8 Visualiser

La visualisation de données est l’un des deux objectifs fondamentaux de R (l’autre étant évidemment de faire des statistiques). Il existe plusieurs méthodes et packages pour produire rapidement et simplement des graphiques. Beaucoup de matériel se retrouve en ligne pour maîtriser les graphiques, mais surtout les personnaliser. L’objectif, bien modeste, de cette section n’est pas de rendre le lecteur maître de la production de figures, mais bien de lui faire faire ses premiers pas et de l’outiller pour qu’il puisse produire simplement et rapidement des graphiques de qualité.

L’exemple de cette section est basé sur celui de la section Manipuler. Voici la syntaxe pour obtenir le jeu de données de nouveau.

jd <- starwars %>% 
  select(name, sex, mass, height, species) %>% 
  filter(species == "Human") %>% 
  na.omit() %>% 
  mutate(height = height  / 100) %>% 
  mutate(IMC = mass / height^2)

8.1 ggplot2

Le package ggplot2 est une extension du tidyverse avec lequel il est possible de créer simplement et rapidement des graphiques. Ces graphiques sont de qualité de publications, idéale pour les articles scientifiques. Le package fournit un langage graphique pour la création intuitive de graphiques compliqués. Il permet à l’utilisateur de créer des graphiques qui représentent des données numériques et catégorielles univariées et multivariées.

La logique de ggplot2 repose sur la grammaire des graphiques (Grammar of Graphics), l’idée selon laquelle toutes les figures peuvent être construites à partir des mêmes composantes. Il s’agit de la deuxième version du package. Voilà pour l’appellation ggplot2.

Dans la grammaire de graphique, une figure possède huit niveaux, dont les trois principaux sont les suivants :

data, les données utilisées;
mapping (aesthetic), cartographier les variables, c’est-à-dire, établir la carte des variables (abscisses, ordonnées, couleur, forme, taille, etc.);
geometric représentation, la représentation géométrique ou le type de représentation graphique, par exemple, diagramme de dispersion, histogramme, boîte à moustache, etc.

Les cinq autres statistics, facet, coordinate space, labels, theme permettent de personnaliser la figure.

Les composantes les plus importantes sont les trois premières, soit les données, la cartographie et la représentation géométrique. Ce sont les éléments de base pour débuter le graphique. Les autres composantes viennent bonifier la figure tout en l’ajustant au besoin de l’utilisateur.

La fonction ggplot() met en place la figure. Le résultat d’utiliser la fonction ggplot() seule est illustrée à la Figure 8.1

ggplot(data = jd)

Figure 8.1: La fonction ggplot() seule - Rien

Il est aussi possible de piper (prononcé avec un fort accent anglophone) les données dans la fonction.

jd %>% 
  ggplot()

Pour afficher des graphiques, il faut ajouter +, puis une représentation géométrique ainsi que la cartographie (mapping). La cartographie (aes(mapping = ), où aes désigne l’esthétisme, aesthetic) peut se trouver dans ggplot() ou dans la représentation géométrique. Si elle est dans ggplot, elle est passée aux autres niveaux.

Voici une liste des représentations géométriques possibles :

geom_line() crée une ligne qui lie toutes les valeurs, très utiles pour une série temporelle (abscisse = temps, ordonnée = variable dépendante);
geom_point() crée un diagramme de dispersion ou un nuage de point, très utile pour les corrélations;
geom_bar() crée un diagramme à bâton, idéal pour présenter des proportions, des fréquences ou des données comptées;
geom_histogram() crée un histogramme des variables;
geom_box() crée une boîte à moustache, idéal pour identifier des valeurs aberrantes et comparer la variabilité entre des groupes;
geom_smooth() crée la ligne de prédiction des données avec des intervalles de confiances, la plupart des utilisateurs voudront certainement ces arguments method = lm (par défaut) ou sans l’erreur standard (se = FALSE);
geom_errorbar() ajoute des barres d’erreur ou des intervalles de confiances spécifiées.

Certaines cartographies sont d’ailleurs compatibles, geom_smooth() et geom_point(), par exemple.

La Figure 8.2 montre un diagramme de dispersion construit à partir du jeu de données jd pipé dans la fonction ggplot(). Dans cette fonction, la cartographie est passée mapping = aes(x = mass, y = height) à un second niveau, geom_point) par le + et la représentation est produite.

jd %>% 
  ggplot(mapping = aes(x = mass, y = height)) + 
  geom_point()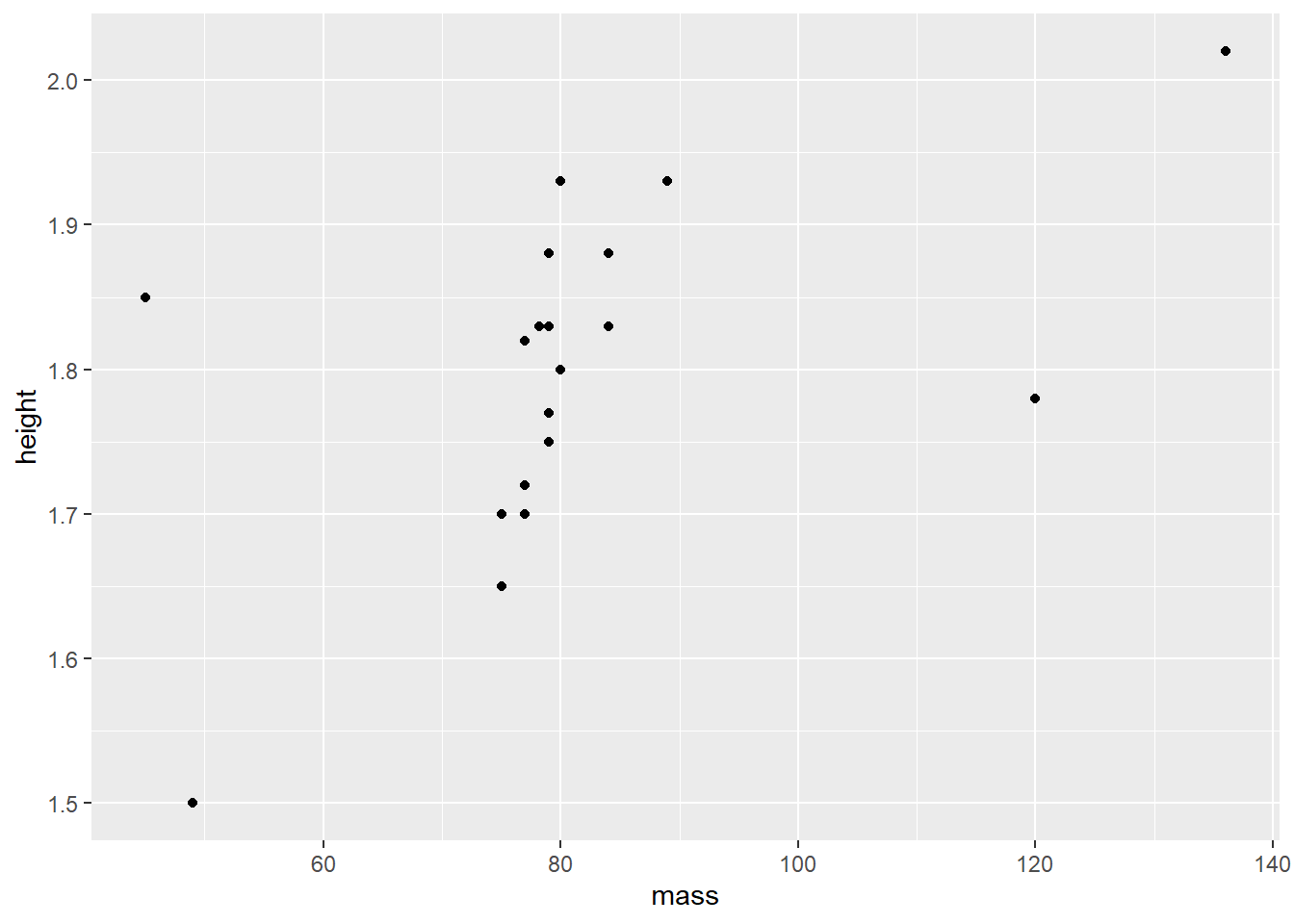

Figure 8.2: Diagramme de dispersion

Voici une liste d’exemples de différentes représentations visuelles des données.

8.2 Diagramme de dispersion

Pour réaliser un diagramme de dispersion, la fonction se nomme geom_point(). La cartographie identifie la variable à l’axe des $x$ (horizontal) et des $y$ (vertical). Dans cet exemple, il s’agit du poids ($x$) et de la taille ($y$). La cartographie ne se limite pas aux axes par contre. Dans cet exemple, la forme shape est aussi un dimension manipulée. Il peut s’agir de color et même de size. Dans la syntaxe ci-dessous, l’argument size est placé à l’extérieur de mapping. Il s’agit alors d’une constante (elle change la taille des points), c’est-à-dire qu’elle ne varie pas relativement à une variable.

jd %>% 
  ggplot() + 
  geom_point(mapping = aes(x = mass, y = height, shape = sex), size = 2)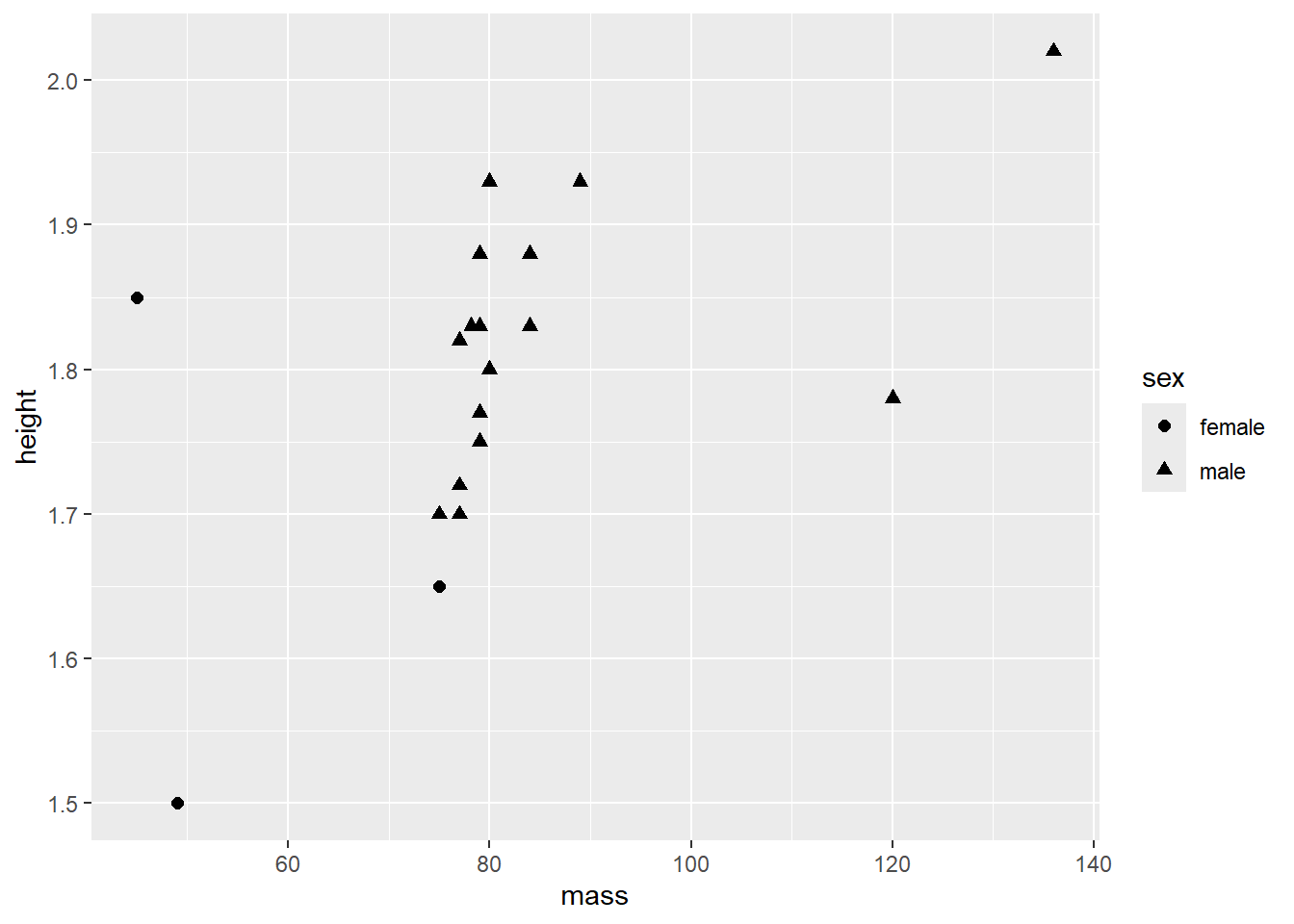

Figure 8.3: Le lien entre le poids et la taille en fonction du sexe

La Figure 8.4 montre le résultat si `size``est ajouté au mapping pour identifier l’IMC. Les unités avec un plus grand IMC obtiennent un plus gros pointeur.

jd %>% 
  ggplot() + 
  geom_point(mapping = aes(x = mass, y = height, shape = sex, size = IMC))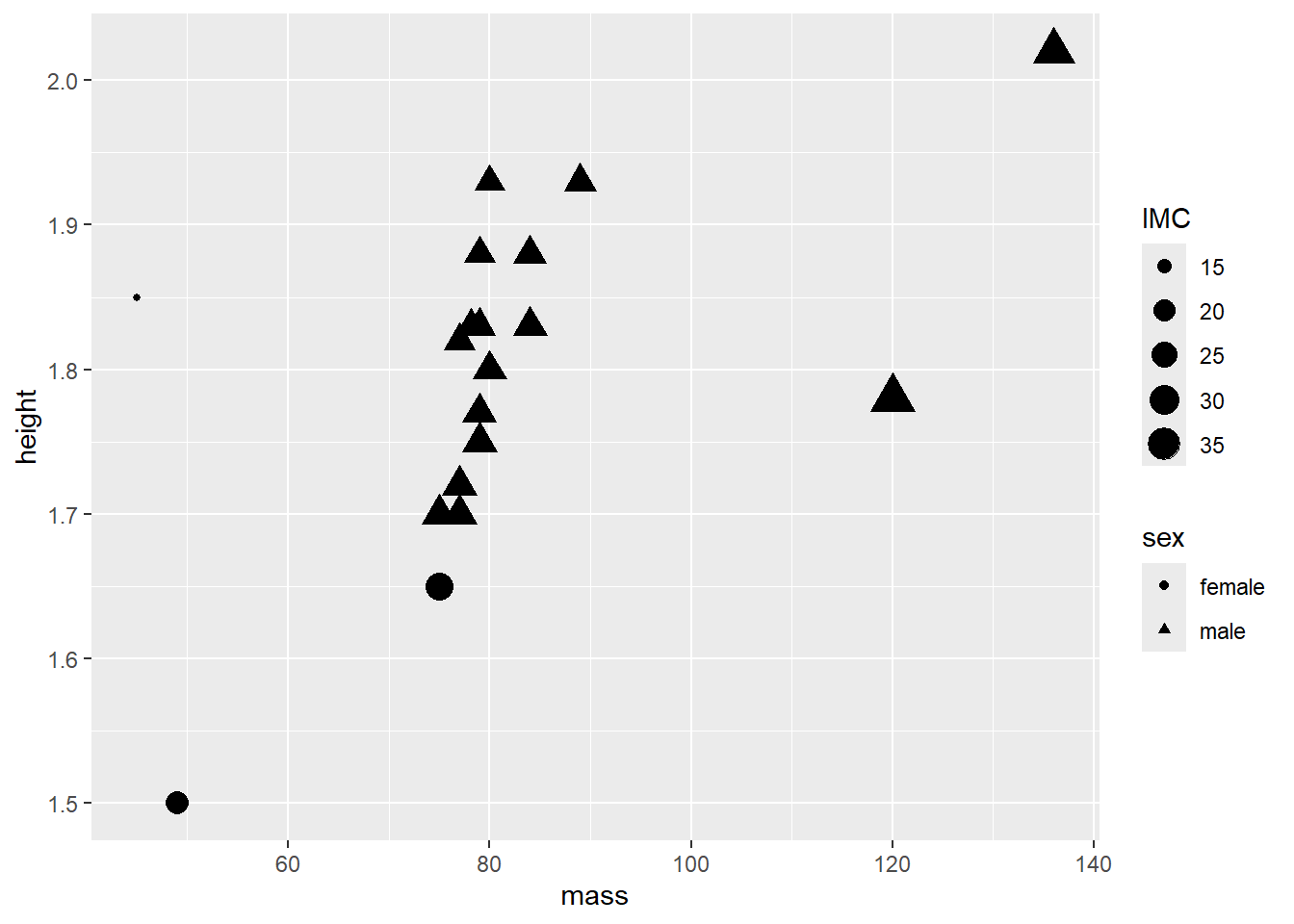

Figure 8.4: Le lien entre le poids et la taille en fonction de l’IMC et du sexe

On peut y ajouter la droite de régression, comme la Figure 8.5 le montre. Sans geom_point(), la figure ne produit la droite. Les arguments de geom_smooth() indique l’utilisation du modèle linéaire, method = lm, et l’absence des intervalles de confiance, se = FALSE. Dans cette syntaxe, comme le mapping est ajouté à ggplot directement, il se généralise directement à geom_point() et geom_smooth()

jd %>% 
  ggplot(mapping = aes(x = mass, y = height)) + 
  geom_point(size = 2) +
  geom_smooth(method = lm, se = FALSE, color = "black")
> `geom_smooth()` using formula = 'y ~ x'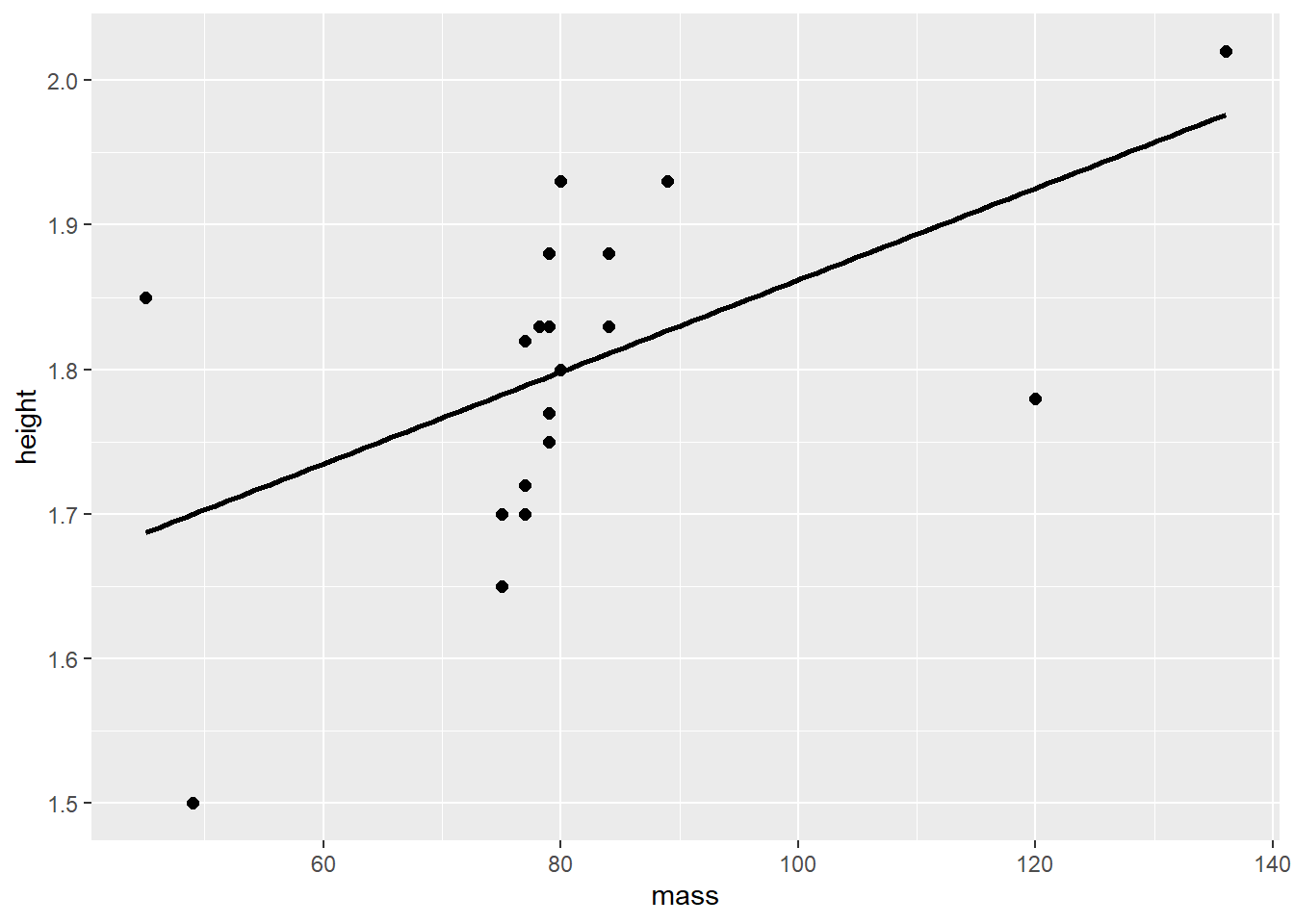

Figure 8.5: Le lien entre le poids et la taille en fonction de l’IMC

8.3 Boîte à moustache

La boîte à moustaches (box-and-whisker plot) est une figure permettant de voir la variabilité des données. Elle résume seulement quelques indicateurs de position soit la médiane, les quartiles, le minimum, et le maximum. Ce diagramme est utilisé principalement pour détecter des valeurs aberrantes et comparer la variabilité entre les groupes. C’est la représentation géométrique geom_boxplot() qui permettra de créer des boîtes à moustache. La cartographie prend en argument une variable nominale en x et une variable continue en y. La Figure 8.6 montre un exemple de boîte à moustache.

ggplot(data = jd) + 
  geom_boxplot(mapping = aes(x = sex, y = IMC)) +
  coord_flip()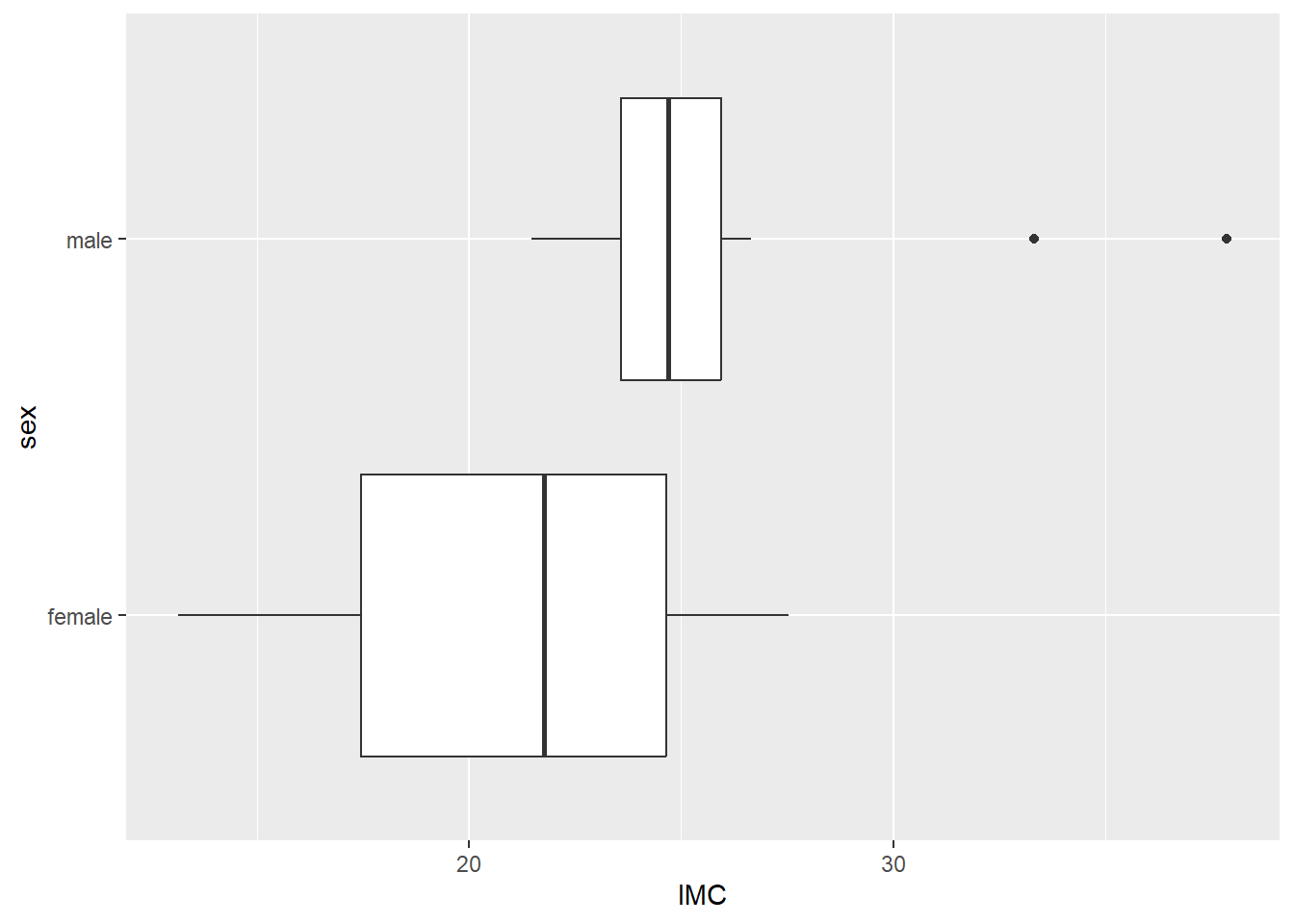

Figure 8.6: Boîte à moustache de l’IMC en fonction du sexe

Une fonction intéressante est la fonction coord_flip() qui tourne (flip) les axes, les coordonnées. L’axe $x$ prend la place de $y$; $y$ prend la place de $x$. Elle peut être pratique pour améliorer la qualité visuelle de certains graphiques.

8.4 Histogramme

Un histogramme permet de représenter la répartition empirique d’une variable. Il donne un aperçu de la distribution sous-jacente, soit comment les données sont distribuées. Cette figure permet de voir la forme de la distribution et permet de voir si elle ne démontre pas d’anomalie. La représentation graphique geom_histogram() produit des histogrammes. S’il faut en produire pour différentes variables, une stratégie simple est de les produire en série.

# Trois histogrammes en trois figures
ggplot(data = jd) + 
  geom_histogram(mapping = aes(x = height))

ggplot(data = jd) + 
  geom_histogram(mapping = aes(x = mass))

ggplot(data = jd) + 
  geom_histogram(mapping = aes(x = IMC))

Des techniques plus avancées permettent de créer la Figure 8.7 d’un seul coup⁸.

# Trois histogrammes en une seule figure
# en optimisant avec le tidyverse
jd %>%
  keep(is.numeric) %>% 
  gather() %>% 
  ggplot(aes(value)) +
  facet_wrap(~ key, scales = "free") +
  geom_histogram()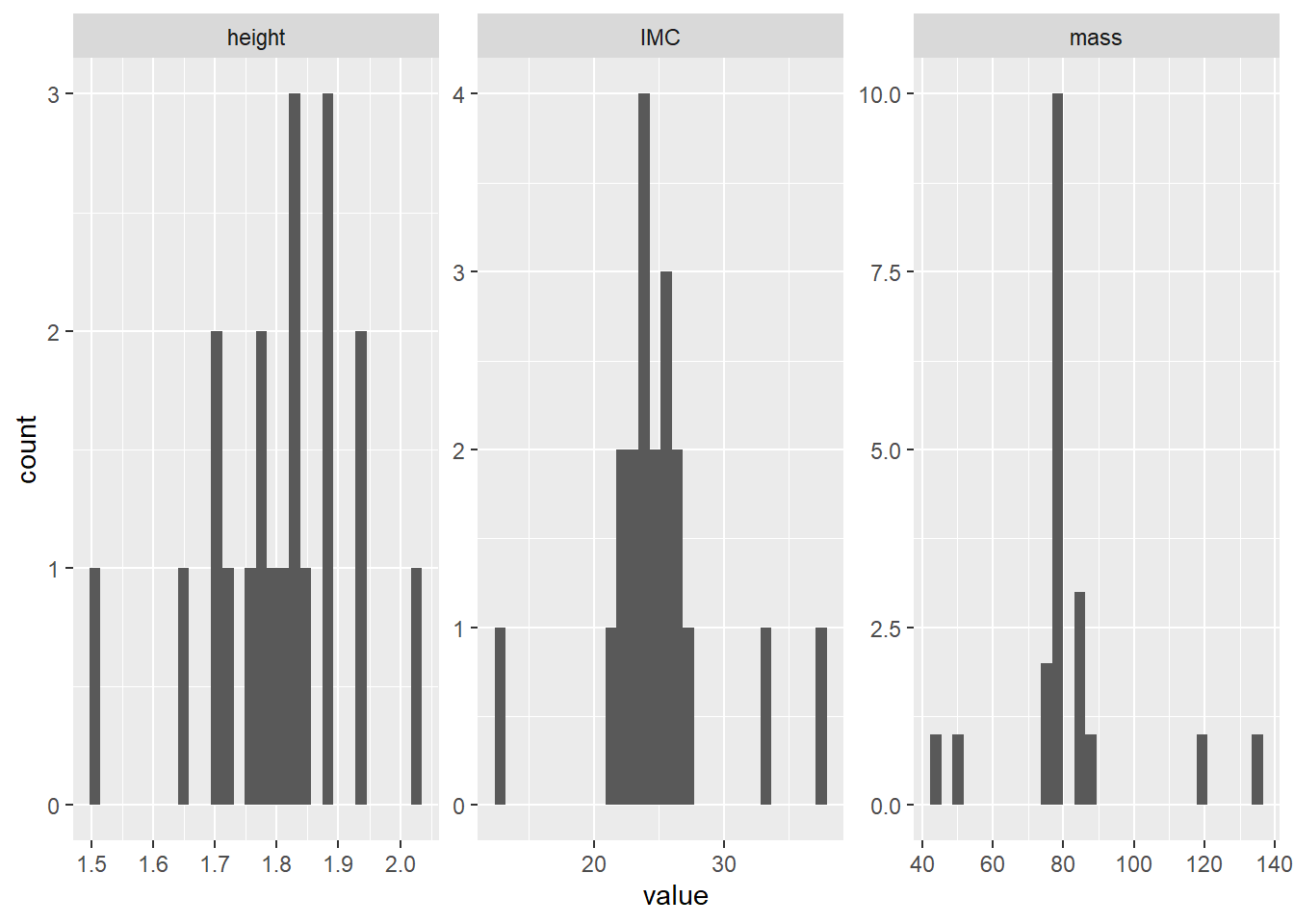

Figure 8.7: Histogrammes des variables continues

Enfin, s’il est désiré de comparer deux distributions de groupes différents, l’argument fill dans la cartographie indique à la fonction de différencier les valeurs selon le remplissage des histogrammes.

jd %>% 
  ggplot(mapping = aes(x = IMC, fill = sex)) + 
  geom_histogram(position = "identity", alpha = .7) + 
  scale_fill_grey()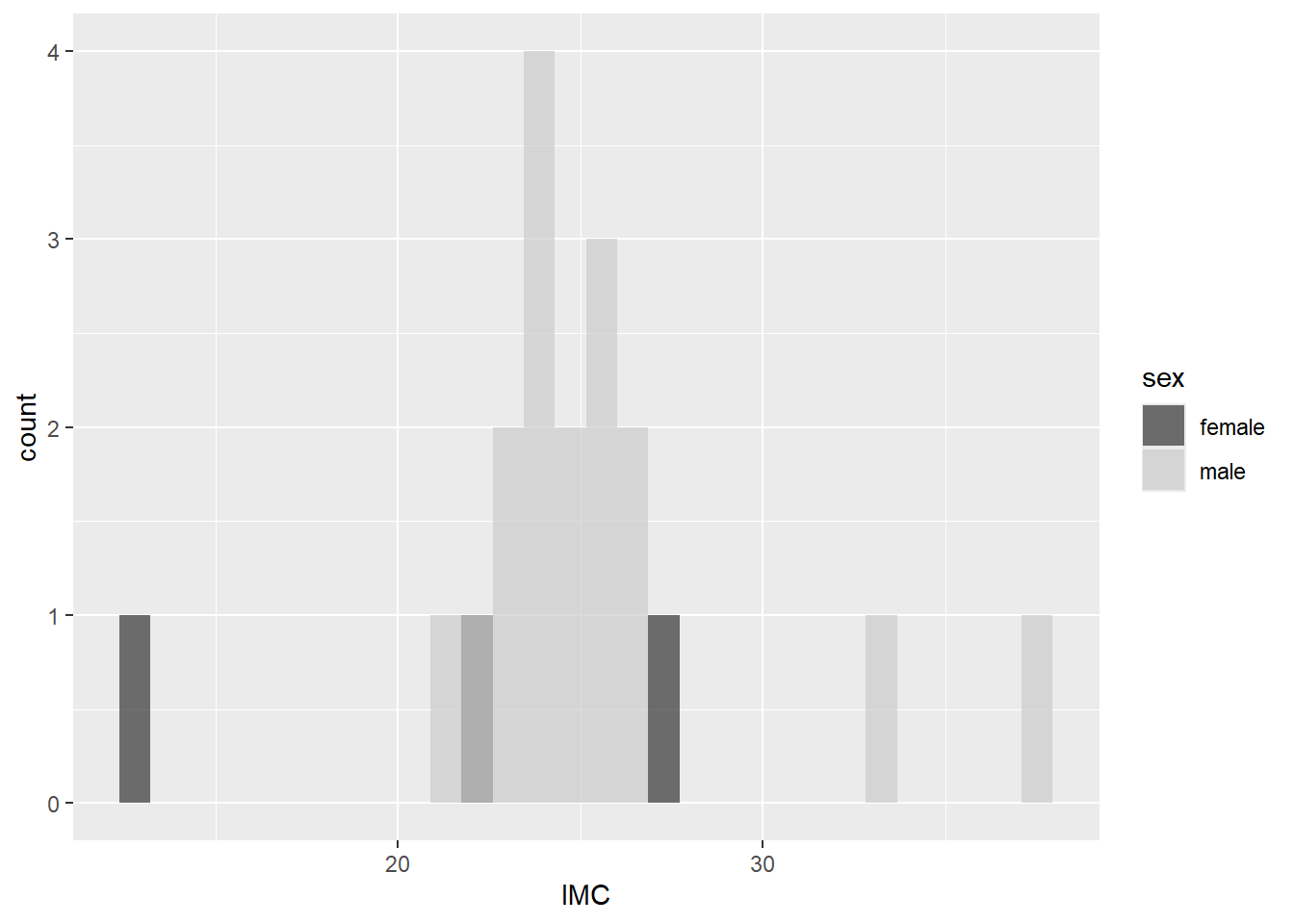

Figure 8.8: Histogrammes de l’IMC par rapport au sexe

Dans la Figure 8.8, l’argument position = "identity" indique de traiter les deux groupes comme différents, autrement les colonnes s’additionnent dans le graphique. L’argument alpha = .7 permet une transparence entre les couleurs, autrement, les valeurs derrière les autres ne paraissent pas. La valeur de alpha va de 0 (transparent) à 1 (opaque) et fonctionne dans la plupart des contextes, surtout ceux liés à ggplot2.

8.5 Les barres d’erreurs

Les barres d’erreur sont une représentation géométrique à part entière. La fonction pour les commandées est geom_errorbar(). Elle nécessite deux arguments, soit l’intervalle de confiance maximale et minimale autour des moyennes à afficher.

La Figure 8.9 illustre les différences entre moyennes avec des barres d’erreur à partir de la base de données ToothGrowth, une étude de l’effet de la vitamine C (dose) selon leur administration (jus ou supplément supp) sur la longueur des dents des cochons d’inde. Il y a deux facteurs et une variable continue.

La première étape est de tirer les statistiques sommaires, moyennes, écart type, tailles des groupes. La syntaxe tire profit de group_by() pour tirer les groupes et en faire le sommaire. Le sommaire summarise permet d’obtenir les statistiques, notamment la moyenne, l’erreur standard (se) pour en calculer l’intervalle autour de la moyenne ci.

stat.descr <- ToothGrowth %>% 
  group_by(dose, supp) %>% 
  summarise(mlen = mean(len),
            sdlen = sd(len),
            nlen = n(), 
            se = sd(len)/sqrt(n()), 
            ci = qt(.975, df = n()-1) * se,
            .groups = "drop")

stat.descr %>% 
  ggplot(aes(x = dose,
             y = mlen, 
             shape = supp),
         size = 5) + 
    geom_errorbar(aes(ymin = mlen - ci,
                      ymax = mlen + ci), 
                  width = .05) +
    geom_line() +
    geom_point()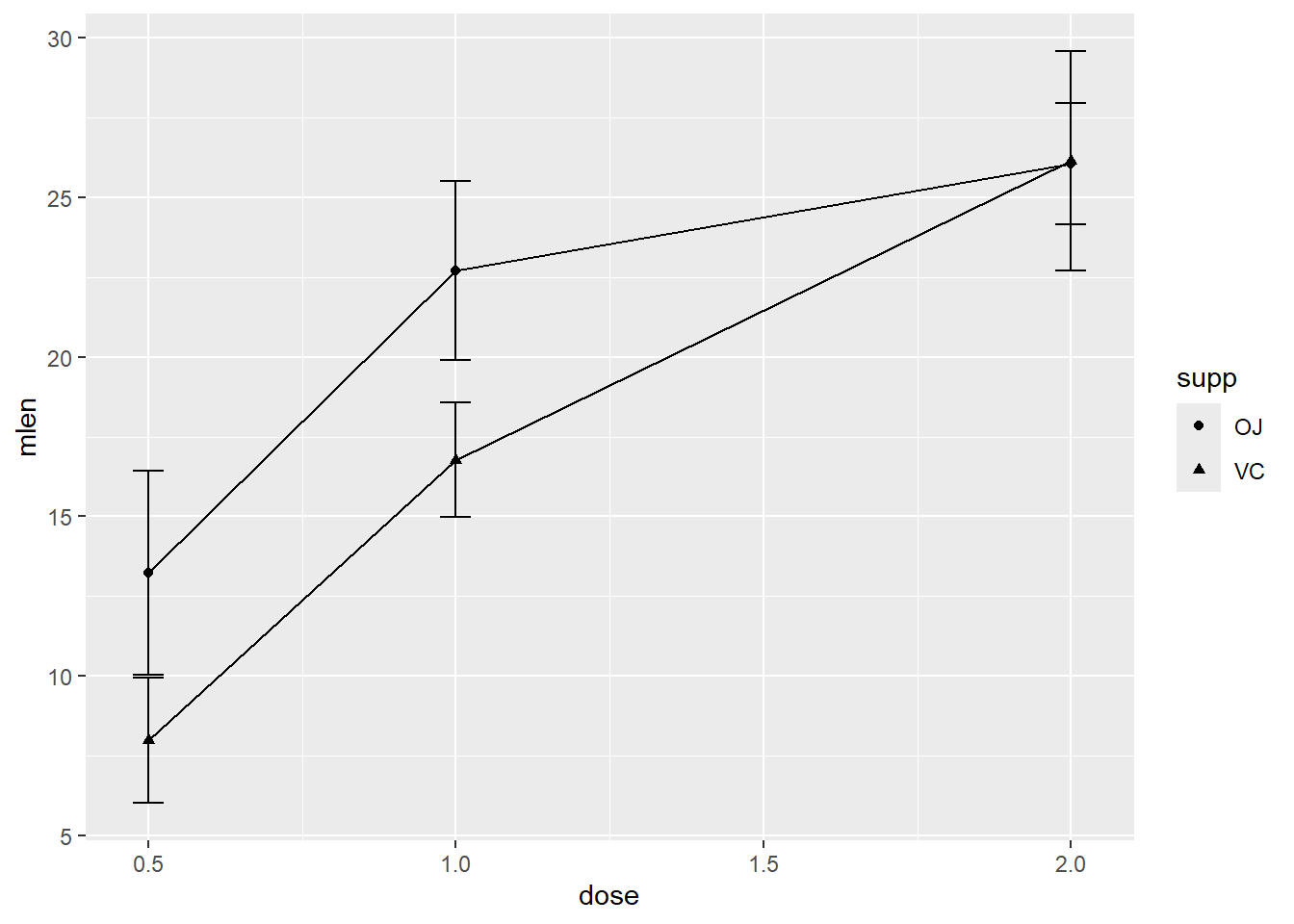

Figure 8.9: Les effets de la vitamine C sur les cochons d’inde

Une fois ces statistiques calculées et enregistrées dans le nouveau jeu de données jd, il est possible de créer le graphique avec les représentations géométriques désirées. Remarquez comment spécifier la cartographie dans le niveau ggplot() rend la syntaxe moins compliquée. Cette syntaxe produit un graphique avec dose à l’axe des $x$, supp comme pointeurs et les moyennes de len (longueur moyenne des dents). La fonction geom_errorbar() indique où placer les limites inférieures et supérieures des intervalles. Les arguments size = 5 et width = .05 sont ajoutés simplment pour l’esthétisme. L’argument .groups = "drop" de summarise permet d’éviter une avertissement expliquant qu’une variable de groupement est utilisé pour regrouper les résultats à la fin. Ajouter ou retirer cet argument ne change pas les calculs, ni la Figure 8.9.

8.6 De meilleures barres d’erreurs pour les devis inter participants

Il existe un package superb (Cousineau et al., 2021) qui permet d’obtenir des graphiques à barre d’erreur avec précision et facilement ajustable. Une fois installé et importé dans l’environnement, superb offre la fonction principale superbPlot permet la création de ces figures.

Il y a deux avantages principaux a utilisé superb. La première est qu’elle permet des ajustements avec l’argument adjustments afin de préciser le type de barres d’erreurs⁹, comme "single", "difference", ou "tryon". Généralement, ce sera l’option purpose = "difference" qui sera désirée. Deuxièmement, superb tient aussi compte des devis intra participants avec l’argument WSFactors, ce qui permet l’utilisation de différentes techniques de décorrélation des temps de mesure. La fonction produit de bien meilleurs graphiques à barres d’erreurs avec plus d’ajustement et de précision.

La Figure 8.10 reproduit la Figure 8.9. Dans le code, il faut préciser les facteurs inter participants BSFactors (pour between subject ou BS) et la variable dépendante, variable. La fonction contrôle aussi le type de graphique avec plotStyle.

library(superb)
superbPlot(ToothGrowth, 
    BSFactors = c("dose","supp"), 
    variables = "len",
    plotStyle = "line")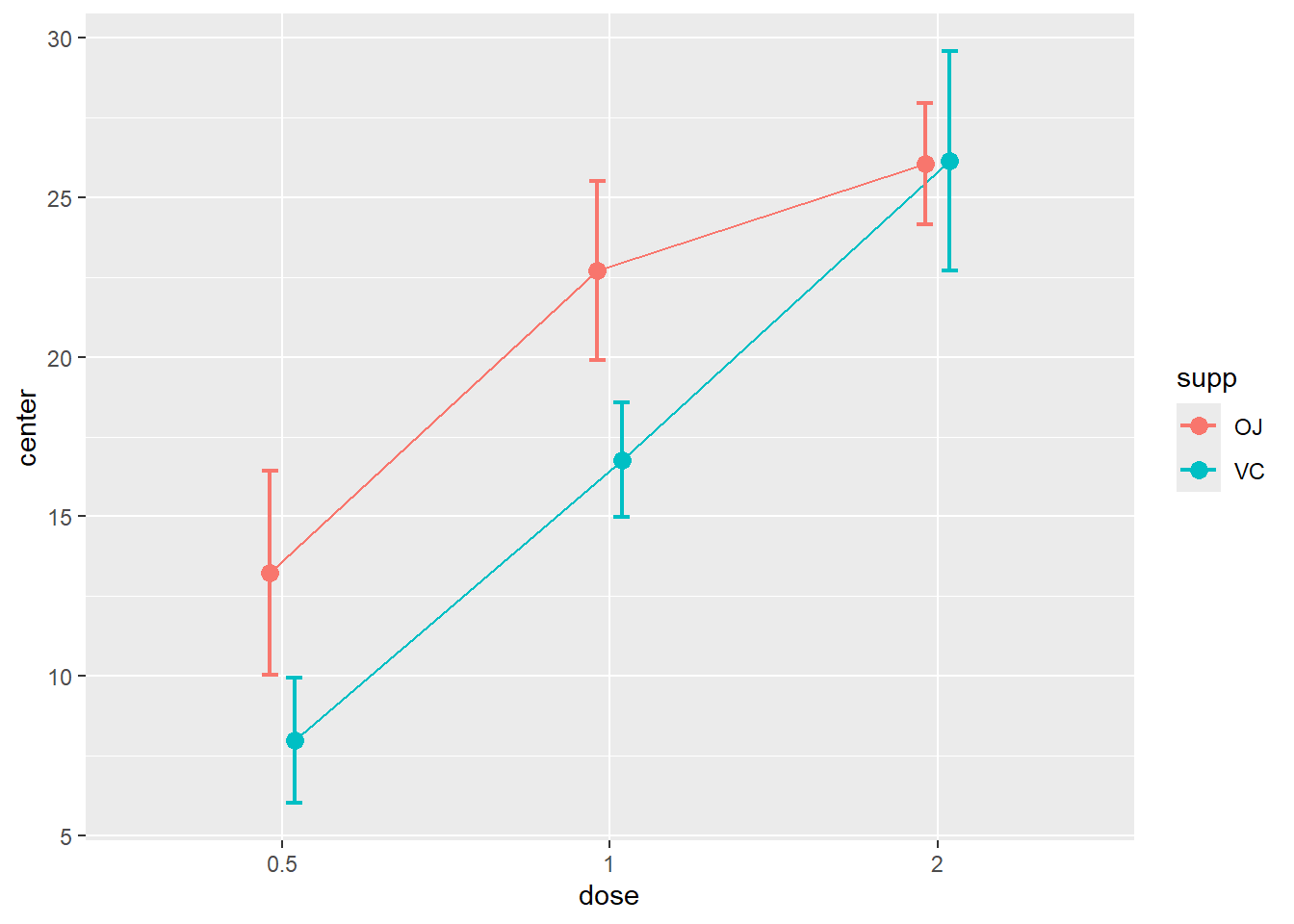

Figure 8.10: Les effets de la vitamine C sur les cochons d’inde avec superb

La fonction retourne souvent des messages d’avertissement (orange) pour préciser certaines décisions qu’elle peut avoir pris. Le code ci-dessus retourne le message : superb::FYI: The variables will be plotted in that order: dose, supp (use factorOrder to change).. C’est à l’utilisateur d’en prendre note et de s’assurer que c’était bien ce qui était désiré, ce qui est le cas ici.

Pour plus de flexibilité pour l’utilisateur, les statistiques descriptives peuvent être obtenues afin de produire personnellement les figures, comme cela avait été fait dans le premier exemple sur Les barres d’erreurs.

stat.descr <- superbData(ToothGrowth, 
                         BSFactors = c("dose","supp"), 
                         variables = "len",
                         adjustments = list(purpose = "difference"))

Attention! Cette variable est une liste contenant deux éléments, les statistiques descriptives ($summaryStatistics) et les données brutes ($rawData). Elle peuvent être extraites avec le signe $, comme stat.descr$summaryStatistics.

Pour reproduire la Figure 8.9 avec le jeu de données extrait de superbData(), il faut procéder à quelques ajustements, comme le nom des variables qui ne sont pas les mêmes, et le fait que la variable dose est maintenant traitée en variable nominale, alors qu’il est souhaitable qu’elle soit numérique pour utiliser la représentation géométrique geom_line(). La Figure 8.11 illustre le résultat.

stat.descr$summaryStatistics %>% 
  ggplot(aes(x = as.numeric(dose),
             y = center, 
             shape = supp),
         size = 5) + 
    geom_errorbar(aes(ymin = center + lowerwidth,
                      ymax = center + upperwidth), 
                  width = .05) +
    geom_line() +
    geom_point()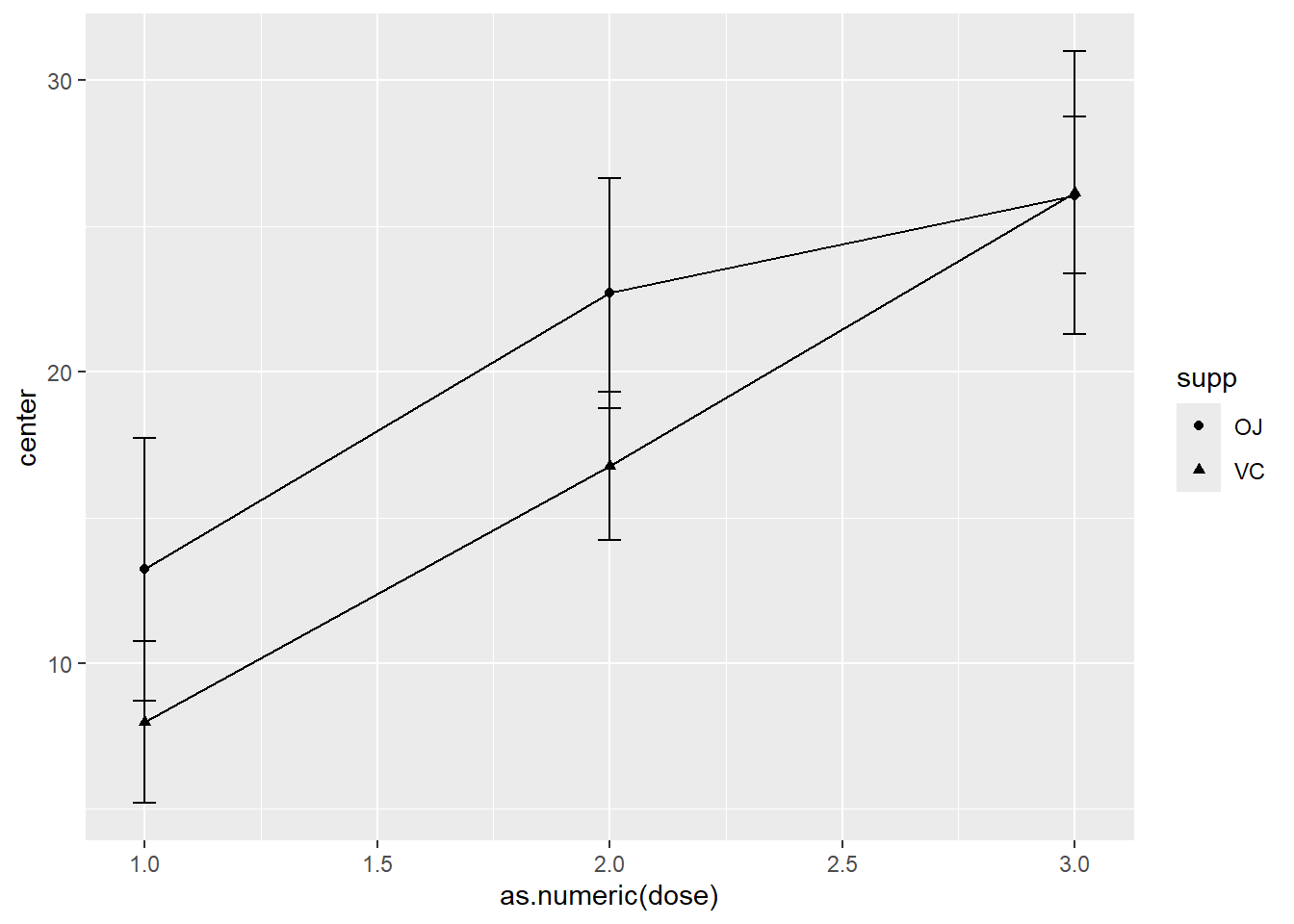

Figure 8.11: Les effets de la vitamine C sur les cochons d’inde avec superb

8.7 De meilleures barres d’erreur pour les devis intra participants

La fonction superbPlot() permet non seulement de produire des barres d’erreurs pour les devis inter participants (deux ou plusieurs groupes de participants différent dans chaque groupe), mais également pour les devis intra partipants (les mêmes participants mesurés plusieurs fois). Elle excelle d’ailleurs dans ce domaine, car elle permet d’ajuster pour type d’intervalle de confiance désiré, mais aussi pour l’ajustement intra participant.

Voici un jeu de données synthétiques pour réaliser une figure avec un devis intra participant. Voir Le test-$t$ dépendant pour plus de détails sur la création de ces données.

# Un exemple de jeu de données
set.seed(148)
temps1 <- rnorm(n = 25, mean = 0, sd = 2)
difference <- rnorm(n = 25, mean = 2, sd = 2)
temps2 <- temps1 + difference
jd_intra <- data.frame(temps1 = temps1,
                 temps2 = temps2)

Pour produire la figure, il faut définir le facteur intra participant (within subject ou WS) par l’argument WSFactors. Cette argument est particulier, il nécessite un mot arbitraire pour identifier l’effet temporelle, ici WSFactors = "temps, mais aussi entre parenthèses, le nombre de temps de mesures, ici "(2)", ce qui forme l’argument complet WSFactors = "temps(2)". Ensuite, pour la variable dépendante, on combine ensemble tous les temps de mesure spécifiés, ici variables = c("temps1", "temps2"). Il reste à définir le style de graphique et les ajustements. Pour l’objectif (purpose), ce sont les mêmes options que pour les devis inter participants, soit ("single", "difference" ou "tryon").

superbPlot(jd_intra, 
    WSFactors = "temps(2)", 
    variables = c("temps1", "temps2"),
    plotStyle = "line",
    adjustments = list(purpose = "difference"))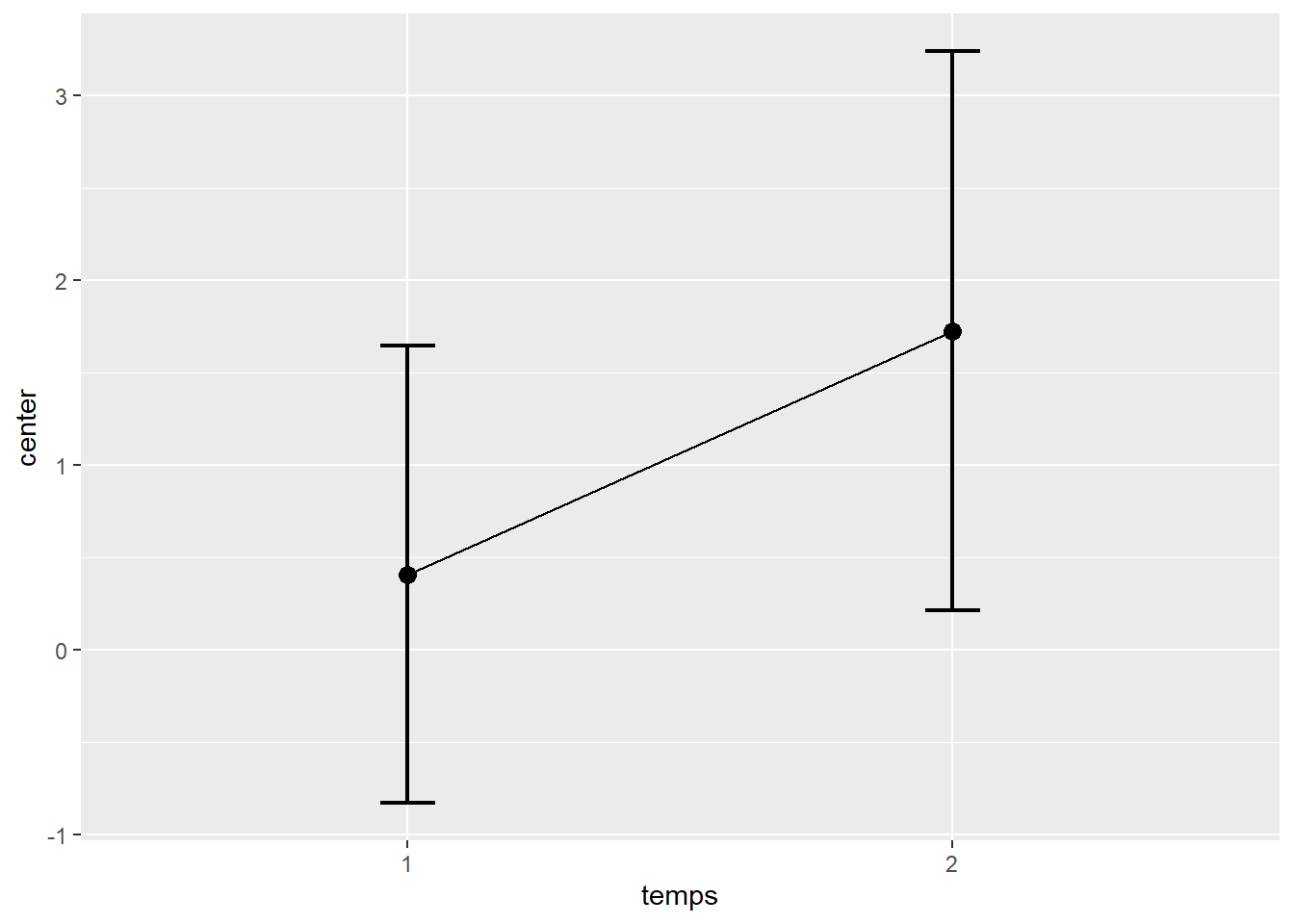

Figure 8.12: Comparaison de deux temps de mesure avec superb (sans décorrélation)

La Figure 8.12 montre le résultat obtenu.

Le package superb permet aussi l’utilisation de techniques de décorrélation comme "CM", "LM", "CA" ou "none" (par défaut) pour améliorer les intervalles de confiance. Consultez la documentation pour en savoir plus sur son fonctionnement et ce qui conviendra le mieux à la situation qui se présente. Pour l’implantation, il suffit d’ajouter à la liste d’arguments fournie à adjustements, le type de décorrlation désirée, ici decorrelation = "CM").

superbPlot(jd_intra, 
    WSFactors = "temps(2)", 
    variables = c("temps1", "temps2"),
    plotStyle = "line",
    adjustments = list(purpose = "difference", decorrelation = "CM"))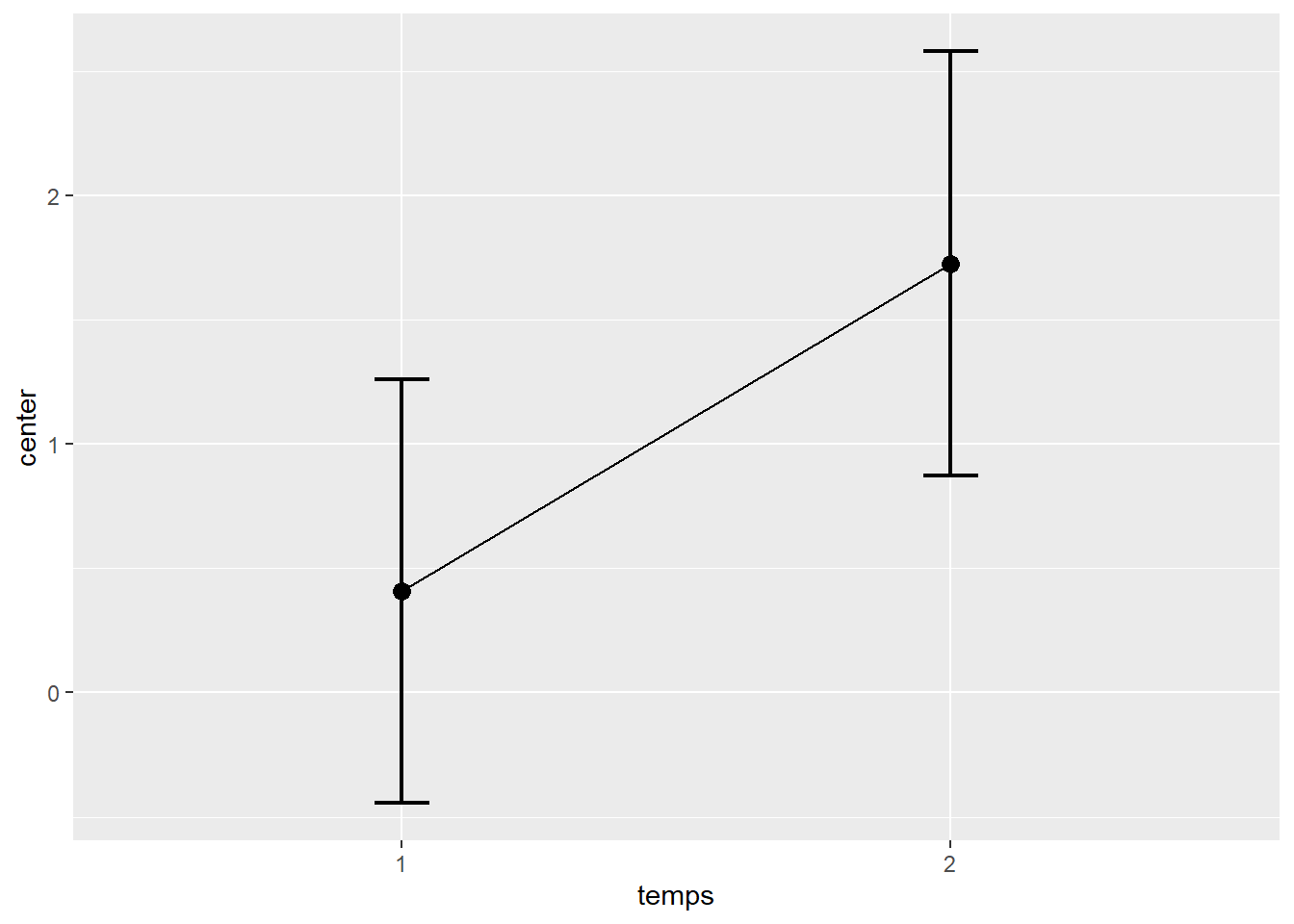

Figure 8.13: Comparaison de deux temps de mesure avec superb (avec décorrélation)

Les barres d’erreur de la Figure 8.13 sont légèrement différentes de la Figure 8.12, mais plus adéquates pour illustrer les résultats.

8.8 Quelques trucs en rafale

Il est possible de renommer les axes avec xlab() et ylab() et le titre avec labs().

Plusieurs ajustements des axes sont possibles avec scale_y_continuous() et scale_x_continuous() et leur équivalent nominal scale_y_discrete(), scale_x_discrete() , comme ajuster les limites (limits), les marqueurs (breaks) et les libellées des marqueurs (labels).

Il est possible de séparer une Figure en différents cadran en spécifiant une variable de séparation avec facet_wrap() ou facet_grid().

8.9 Exporter la figure

Pour exporter une figure, ggplot2 offre la très conviviale fonction ggsave() qui permet d’enregistrer la dernière figure produite en fichier. Celle-ci vient avec plusieurs options pour gérer l’enregistrement.

L’option filename gère le nom du fichier le nom et le type de fichier, comme les usuels "pdf", "jpeg", "png", ou les moins fréquents, mais aussi pratiques "bmp", "eps", "tiff", "ps", "tex", "svg" et "wmf".

Les options width (largeur), height (hauteur), et units (unités, comme "in", pouce, "cm", centimètre, "mm", millimètre ou "px", pixel) gère la taille de la figure.

La taille de résolution de la figure est gérée avec l’argument dpi, ce qui peut être utile pour augmenter la qualité de la figure produite.

Voici un exemple.

# Préalablement produire une figure
ggsave(filename = "mafigure.pdf",
       width = "6"
       heigth = "8",
       unit = "cm")

Il faudra éventuellement ajuster la taille et la qualité de la figure en fonction de la sortie désirée. Quelques essais seront probablement nécessaires pour y arriver.

8.10 Pour aller plus loin

Il existe une multitudes de livres, de sites web, de tutoriels en ligne et d’atelier pour donner l’occasion au lecteur d’aller plus loin dans sa conception graphique. Voici quelques ouvrages de références : Le R Graphics Cookbook (Chang) repérable à https://r-graphics.org/, ggplot2: elegant graphics for data analysis (Wickham) repérable à https://ggplot2-book.org/ ou R Graphics (Murrel) repérable à https://www.stat.auckland.ac.nz/~paul/RG2e/.

7 Manipuler

Exercices