Solutions
Rudiments
Question 1
- Quel est le résultat de
mean <- c(1, 2, 3)? Pourquoi?
Le résultat est \(1, 2, 3\). Le fait d’assigner une valeur à une fonction (ou variable) écrase cette dernière.
Voir Les variables pour plus de renseignements.
Question 2
- Quelle est la différence entre
# Caractèreet"Caractère"?
Le premier est une commentaire (voir Les commentaires) alors que le second est une chaîne de caractère (voir Les chaînes de caractère).
Question 3
- Créer un vecteur contenant les valeurs \(4, 10, 32\). Calculer la moyenne et l’écart type de ce vecteur.
Voir Concaténer pour créer un vecteur et la moyenne et l’écart type pour plus d’informations.
Question 4
- Créer un vecteur contenant les valeurs de \(4\) à \(11\). Sélectionner la deuxième valeur de ce vecteur, puis additionner 100 à cette valeur et remplacer la dans le vecteur.
vecteur <- 4:11 # ou seq(4, 11)
vecteur[2] <- vecteur[2] + 100Voir Concaténer pour créer un vecteur et Référer à des sous-éléments pour choisir un élément.
Question 5
- Générer 10 valeurs aléatoires distribuées normalement avec une moyenne de 50 et un écart type de 4. Calculer la moyenne, la médiane et la variance.
# Pour la reproductibilité
set.seed(42)
# Créer
x <- rnorm(n = 10, mean = 50, sd = 4)
# La moyenne, la médiane et la variance
mean(x)
> [1] 52.2
median(x)
> [1] 51.5
var(x)
> [1] 11.2Voir Les graines pour la fonction set.seed(), Les distributions pour la fonction rnorm() ainsi que son aide ?rnorm pour les arguments spécifiques, et la moyenne, la médiane et la variance pour plus d’informations.
Question 6
- Créer un jeu de données contenant quatre sujets avec, pour chacun, leur nom de famille, leur âge et un score d’appréciation tiré d’une distribution uniforme allant de 0 à 100.
# Pour la reproductibilité
set.seed(1234)
# Créer
jd <- data.frame(nom = c("Eccleston", "Tennant", "Smith", "Capaldi"),
age = c(41, 35, 28, 55),
score = runif(n = 4, min = 0, max = 100))
# Imprimer le jeu dans la console
jd
> nom age score
> 1 Eccleston 41 11.4
> 2 Tennant 35 62.2
> 3 Smith 28 60.9
> 4 Capaldi 55 62.3Voir Les graines pour la fonction set.seed(), Créer un jeu de données pour data.frame() et Concaténer pour les vecteurs en arguments, Les distributions pour la fonction runif() ainsi que son aide ?runif pour les arguments spécifiques. Les noms sont des chaînes de caractère.
Question 7
- Rédiger une fonction calculant l’hypoténuse d’un triangle rectangle. Rappel: le théorème de Pythagore est \(c^2=a^2+b^2\).
En prenant a et b comme arguments.
Voir Les fonctions pour plus d’informations.
Question 8
- Rédiger une fonction calculant un score-\(z\) pour une variable. Rappel: un score-\(z\), correspond à \(z=\frac{x-\mu}{\sigma}\).
Deux possibilités ici. Soit x est un vecteur contenant plusieurs nombres ou il est un nombre et il faut ajouter la moyenne (\(\mu\)) et l’écart type (\(\sigma\)).
# Premier cas
score.z <- function(x) {
(x-mean(x))/sd(x)
}
# Deuxième cas
score.z <- function(x, mu, sigma) {
(x-mu)/sigma
}
score.z(130, mu = 100, sigma = 15)
> [1] 2Le premier cas est l’équivalent de la fonction scale() qui rempliera la même tâche.
Voir Les fonctions pour plus d’informations. Les scores-\(z\) sont abordés plus en profondeur à la section Inférence avec la distribution normale sur une unité.
Question 9
- Rédiger une fonction calculant la médiane d’une variable (ne pas recopier celle de ce livre).
Voici une autre fonction calculant une médiane d’un vecteur.
mediane <- function(x){
x <- sort(x)
longueur <- length(x)
if (longueur%%2) {
# Si impair
# Prendre la valeur centrale
x[(longueur + 1)/2]
} else {
# Si pair
# Faire la moyenne des deux éléments du centre
mean(x[rep(longueur/2, 2) + 0:1])
}
}Encore une fois (il n’y a pas vraiment de façon de l’éviter), %%2 permet de tester si pair (FALSE, car 0 si pair) ou impair (TRUE, car 1 si impair), puis de prendre la valeur à la position correspondante. Il y a plusieurs façons de tirer les éléments du vecteur.
Voir Les fonctions, mais surtout La médiane, pour plus d’informations.
Question 10
- Rédiger une fonction qui pivote une liste de \(k\) éléments par \(n\). Par exemple, une liste de six (\(k=6\) comme \([1,2,3,4,5,6]\)) pivoté de deux (\(n=2\)) devient (\([3,4,5,6,1,2]\)).
Plusieurs solutions possibles dont en voici une.
Question 11
- Rédiger une fonction pour générer une séquence de Fibonacci (chaque nombre est la somme des deux précédents) jusqu’à une certaine valeur, soit \(1, 1, 2, 3, 5, 8,...\). (Question difficile)
Plusieurs solutions possibles dont en voici deux.
fibonnaci1 <- function(n){
# n est le nombre d'éléments de la série demandée.
# Création d'un vecteur de taille n ne contenant que des 1.
serie <- rep(1, n)
# Le premier test logique rapporte la (n = 1) ou
# les deux (n = 2) premières valeurs.
if(n <= 2){
serie <- serie[1:n]
# Le deuxième réalise les calculs pour les autres options.
}else{
for(i in 3:n){
serie[i] <- serie[i-1] + serie[i-2]
}
}
serie
}En voici une autre en utilisant la récursion (une fonction qui s’appelle elle-même).
fibonnaci2 <- function(n){
if(n <= 2){
# Si n est plus petit que 2, alors retourne 1
1
} else {
# Autrement, retourne les deux valeurs de Fibonncaci précédentes.
fibonnaci2(n-1) + fibonnaci2 (n-2)
}
}Les voici comparées.
Jeux de données
Question 1
- À l’aide de
data_edit()du packageDataEditR, créez un jeu données contenant trois participants ayant les caractéristiques suivantes,nom = Alexandre, Samuel et Vincentetage = 20, 22 et 31.
# Installer et appeler le package DataEditR, si ce n'est fait
jd <- DataEditR::data_edit()La Figure 22.7 montre le résultat dans le tableur.
Figure 22.7: Entrée des données
Question 2
- Prendre le jeu de données
cars, sélectionner la variabledistet transformer la en mètre, plutôt qu’en pieds. Rappel: un mètre égale 3.2808 pieds.
Avec le tidyverse de télécharger.
cars %>% # Le jeu de données
select(dist) %>% # Sélectionner
mutate(dist_m = dist / 3.2808) %>% # Transformer
head() # Montrer les 6 premières lignes
> dist dist_m
> 1 2 0.61
> 2 10 3.05
> 3 4 1.22
> 4 22 6.71
> 5 16 4.88
> 6 10 3.05La fonction head() permet d’afficher seulement les six premières lignes au lieu des 50 du jeu de données.
Question 3
- Dans le jeu de données
iris, calculer la moyenne et l’écart type de la longueur de sépale (Petal.Length) en fonction de l’espèce (species). Représenter ensuite la moyenne à l’aide d’un diagramme à barre
Avec le tidyverse de télécharger.
iris %>%
group_by(Species) %>%
summarise(M = mean(Petal.Length), ET = sd(Petal.Length))
> # A tibble: 3 × 3
> Species M ET
> <fct> <dbl> <dbl>
> 1 setosa 1.46 0.174
> 2 versicolor 4.26 0.470
> 3 virginica 5.55 0.552Voir La moyenne, L’écart type et Manipuler. Il est aussi possible d’utiliser psych::describeBy(iris, group = "Species") (voir Décrire), mais cela offre plus que demandé.
Pour la figure, il faut prendre le résultat de la manipulation précédente et utiliser ggplot2 avec la représentation géométrique geom_col() et la cartographie mapping = aes(x = Species, y = M), ce qui donne l’espèce à l’abscisse et la moyenne (M) à l’ordonnée.
iris %>%
group_by(Species) %>%
summarise(M = mean(Petal.Length), ET = sd(Petal.Length)) %>%
ggplot(mapping = aes(x = Species, y = M)) +
geom_col()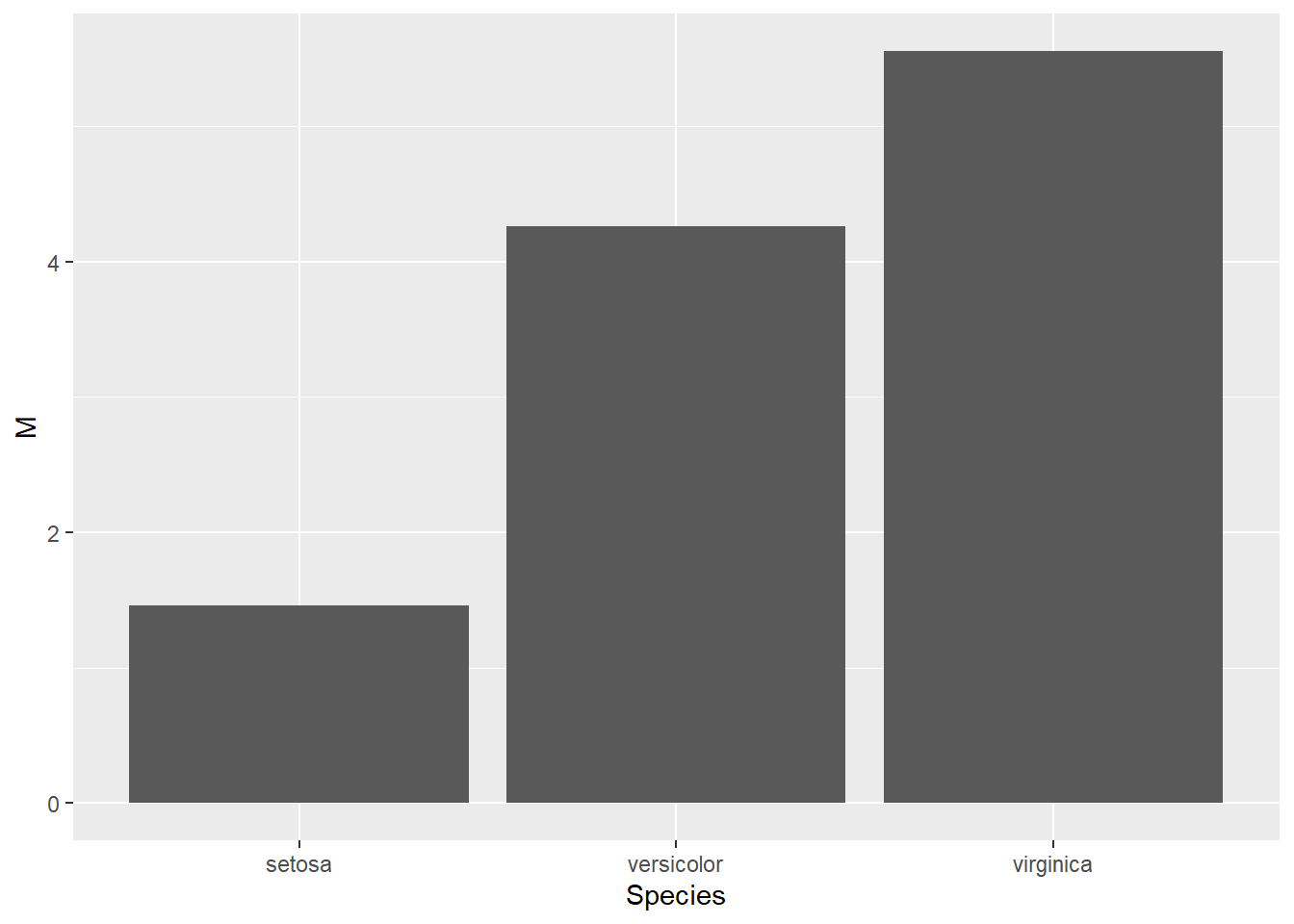
Figure 22.8: M par Espèce (question 3)
Question 4
- Prenez le jeu de données
mtcarset produisez un diagramme de dispersion montrant la puissance brute (en chevaux) (hp) par rapport à consommation en km/l (basé surmpg) tout en soulignant l’effet du nombre de cylindres (cyl). Attention la fonctionas_factorpermettra d’utilisercylen facteur et le rapprt mpg vers kml approximativement \(.425\).
mtcars %>%
mutate(kml = .425 * mpg,
cyl = as_factor(cyl)) %>%
ggplot(mapping = aes(x = hp, y = kml, color = cyl)) +
geom_point()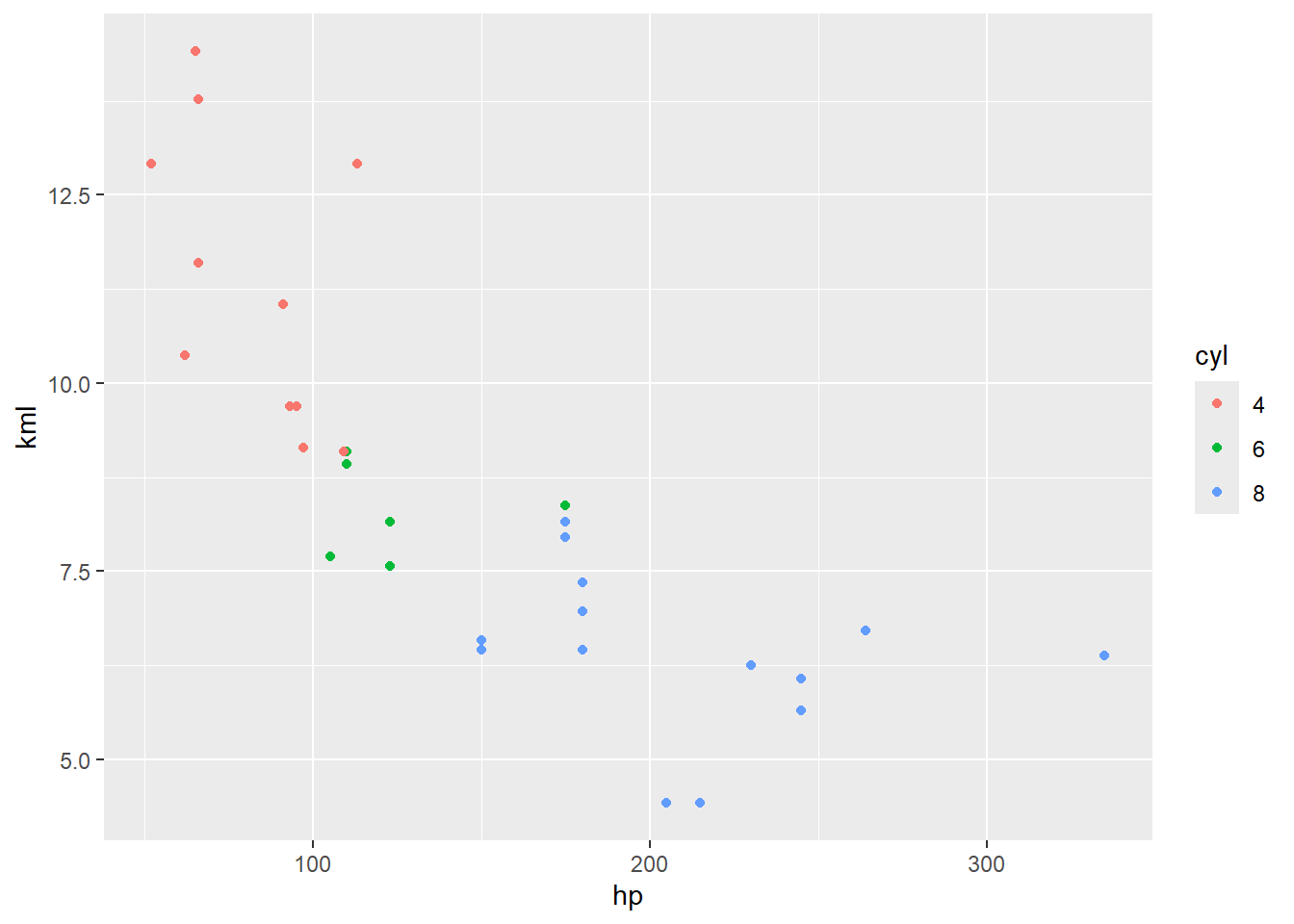
Figure 22.9: Visualisation de kml par hp en fonction de cyl (question 4)
Question 5
- Avec le même jeu de données et objectif que la question précédente, ajouter une droite de prédiction avec
geom_smooth()selon un modèle linéare (lm) et sans erreur standard (se).
mtcars %>%
mutate(kml = .425 * mpg,
cyl = as_factor(cyl)) %>%
ggplot(mapping = aes(x = hp, y = kml, color = cyl)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE)
> `geom_smooth()` using formula = 'y ~ x'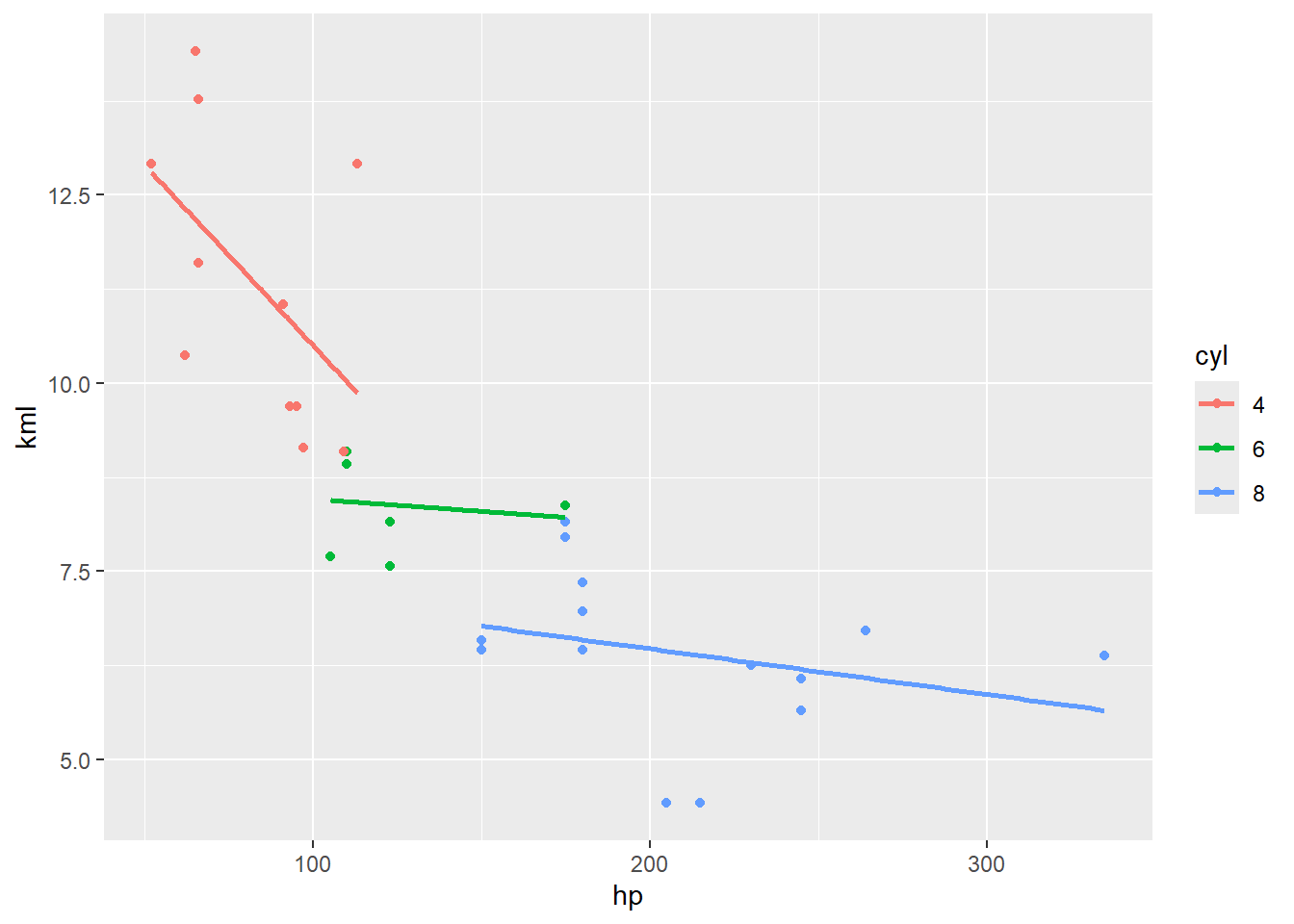
Figure 22.10: Visualisation de kml par hp en fonction de cyl (question 5)
Question 6
- Avec le jeu de données
chickwts, produire une boîte à moustache du poids des poulets en fonction de leur alimentation.
chickwts %>%
ggplot(mapping = aes(x = feed, y = weight)) +
geom_boxplot()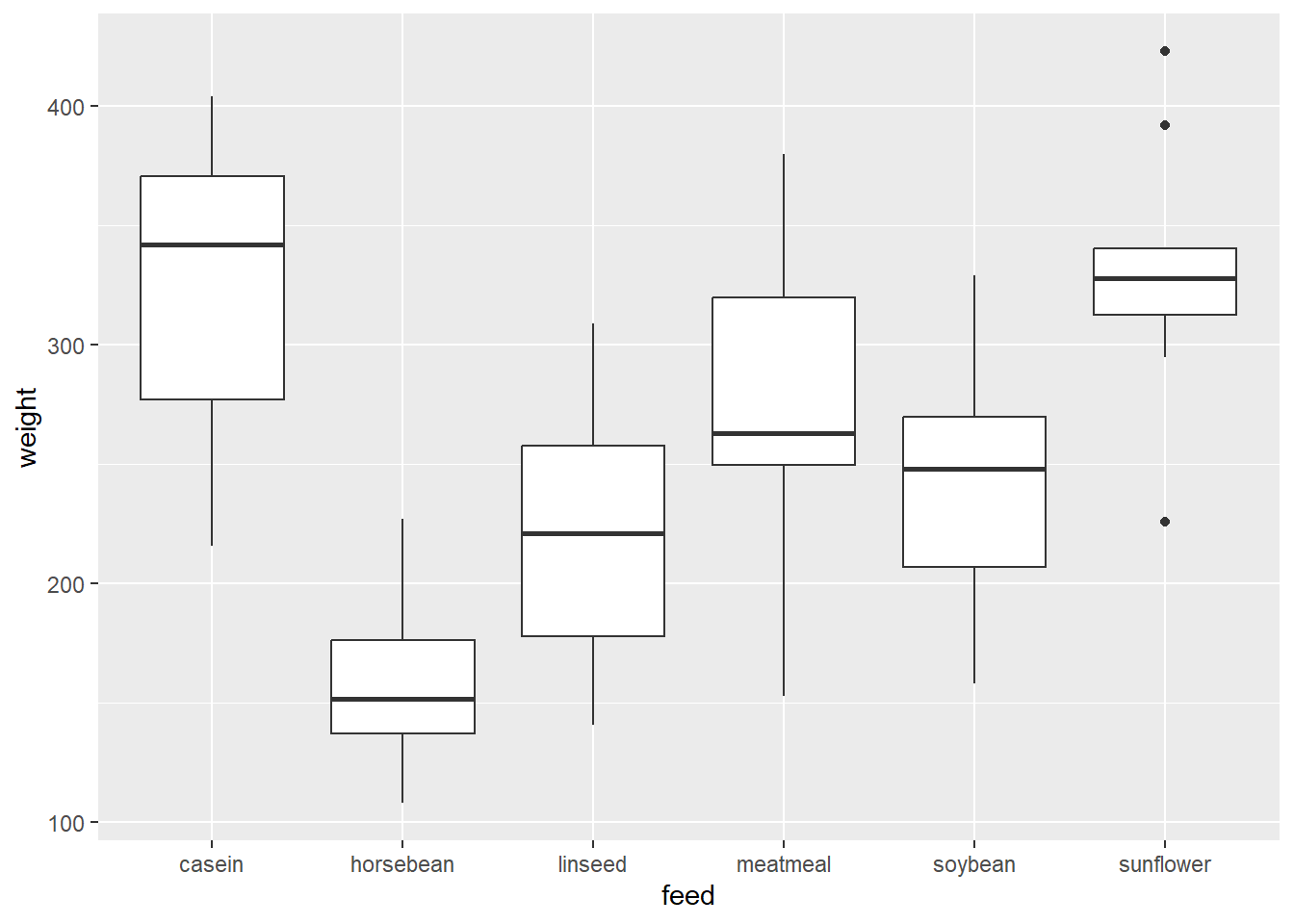
Figure 22.11: Visualiation de weight par feed (question 6)
Dans cette question, l’utilisation du filtre filter(feed %in% c("horsebean", "sunflower")) pourra poser quelques difficultés, mais ne devrait arriver assez rarement en pratique.
Question 7
- Prenez le jeu de données
mtcarset produisez un histogramme montrant la variabilité de la consommationmpgpar rapport à la transmission (am). Attention la fonctionas_factorpermettra d’utiliseramen facteur.
mtcars %>%
mutate(am = as_factor(am)) %>%
ggplot(mapping = aes(x = mpg, fill = am)) +
geom_histogram(bins = 12) # Pour éviter un avertissement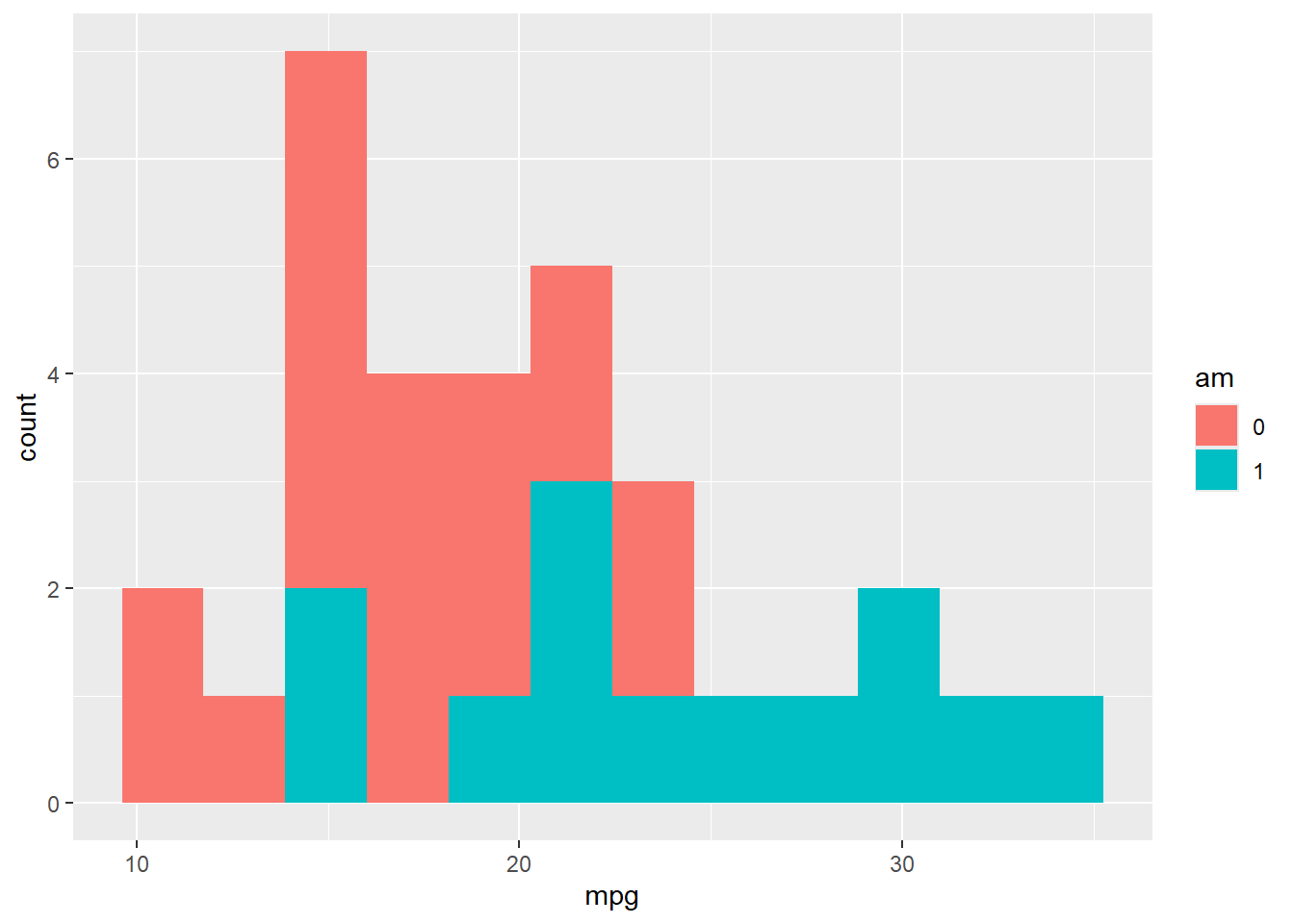
Figure 22.12: Histogramme de mpg par am (question 7-1)
Noter que bins = 12 ne sert qu’à éviter un avertissement.
Pour avoir les histogrammes dans des cadrans différents, la fonction facet_wrap() est utile.
mtcars %>%
mutate(am = as_factor(am)) %>%
ggplot(mapping = aes(x = mpg)) +
geom_histogram(bins = 12)+
facet_wrap(~am)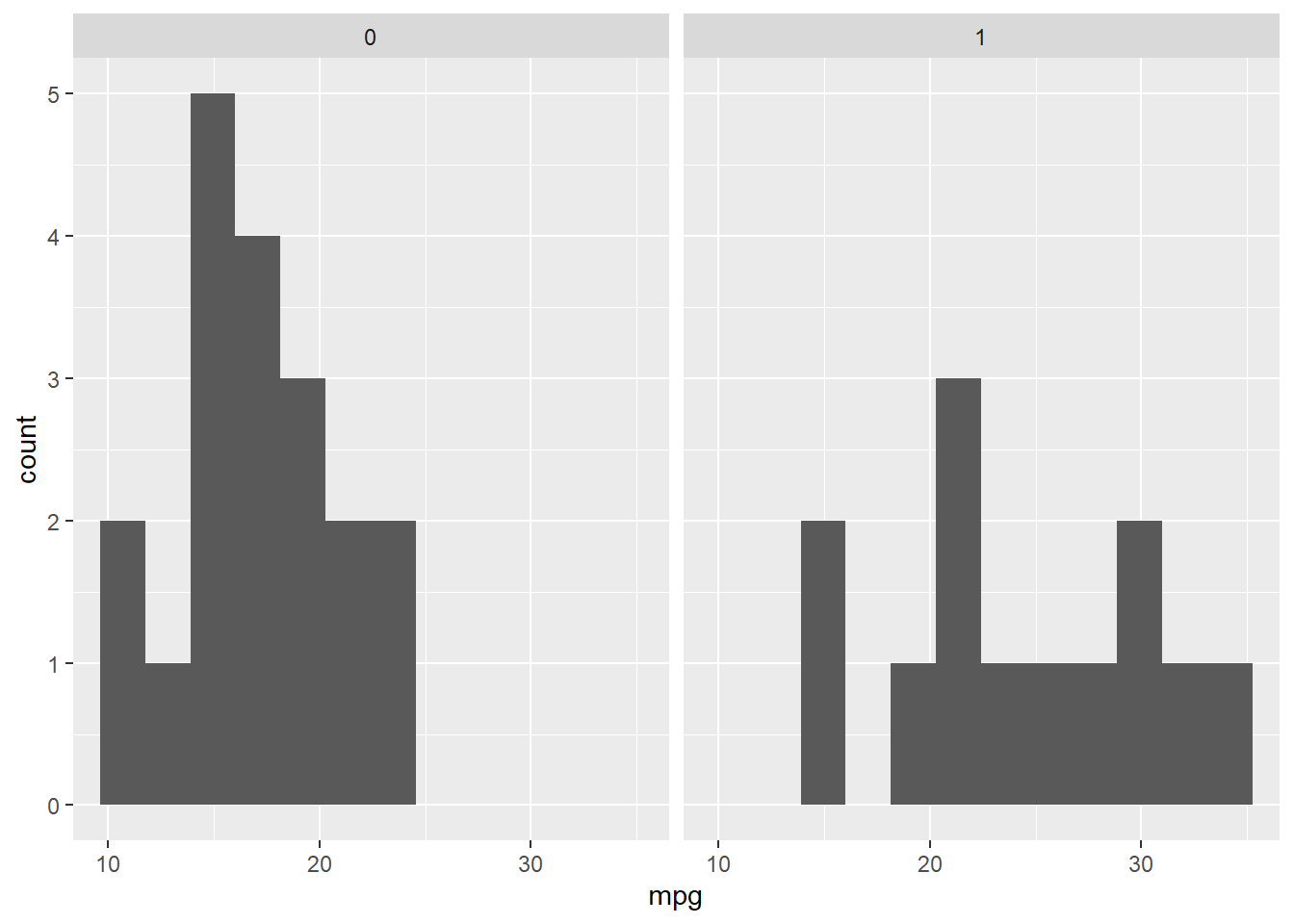
Figure 22.13: Histogramme de mpg par am (question 7-2)
Question 8
- Prendre le jeu de données
msleepet produire un diagramme à barres pour observer la fréquence des régimes alimentaires.
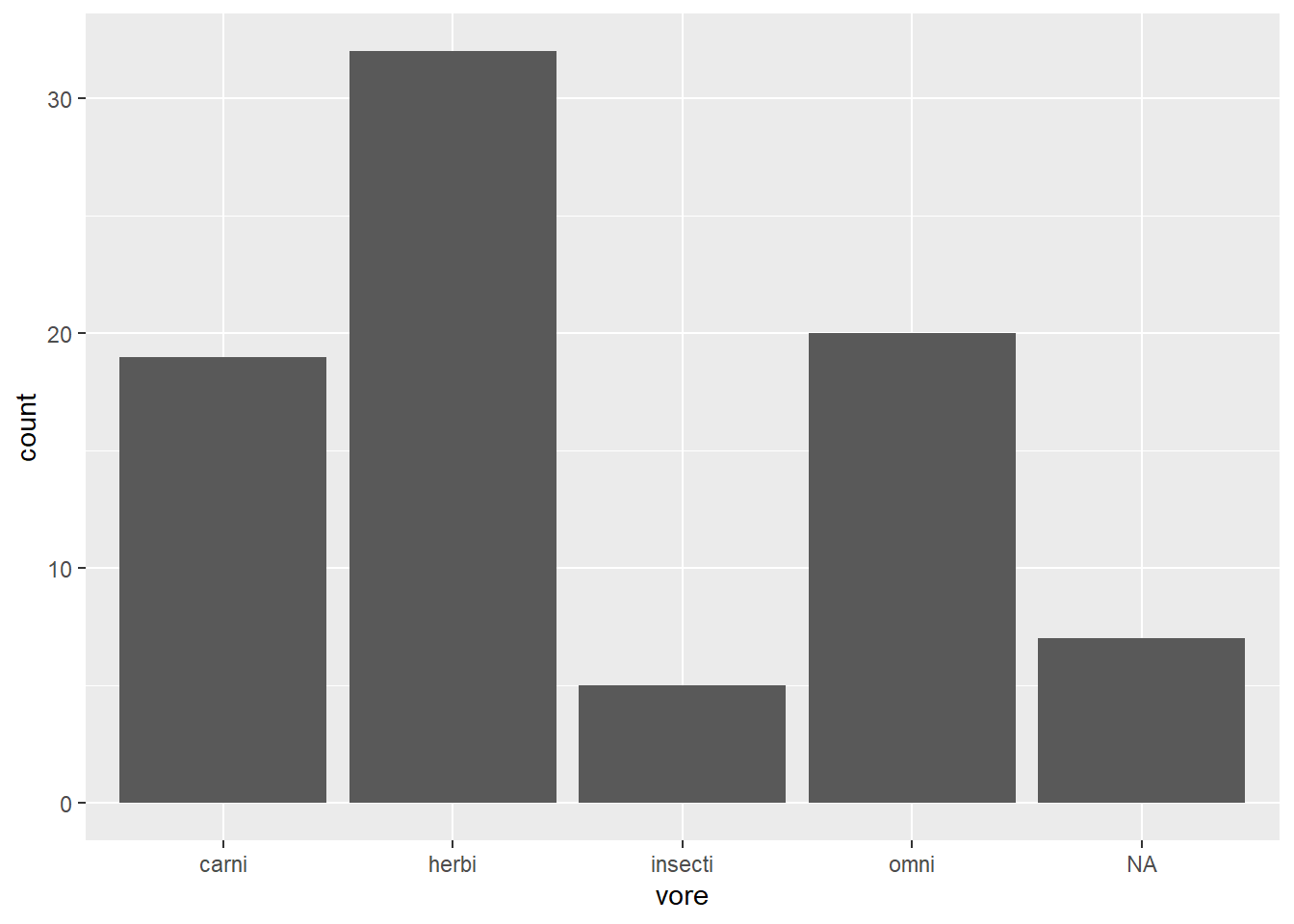
Figure 22.14: Diagramme à barre du régime alimentaire (question 8)
Question 9
- Prendre le jeu de données
msleepet produisez une boîte à moustache pour observer le temps total de sommeil (sleep_total) moyen par rapport aux régimes (vore). Attention aux données manquantes.
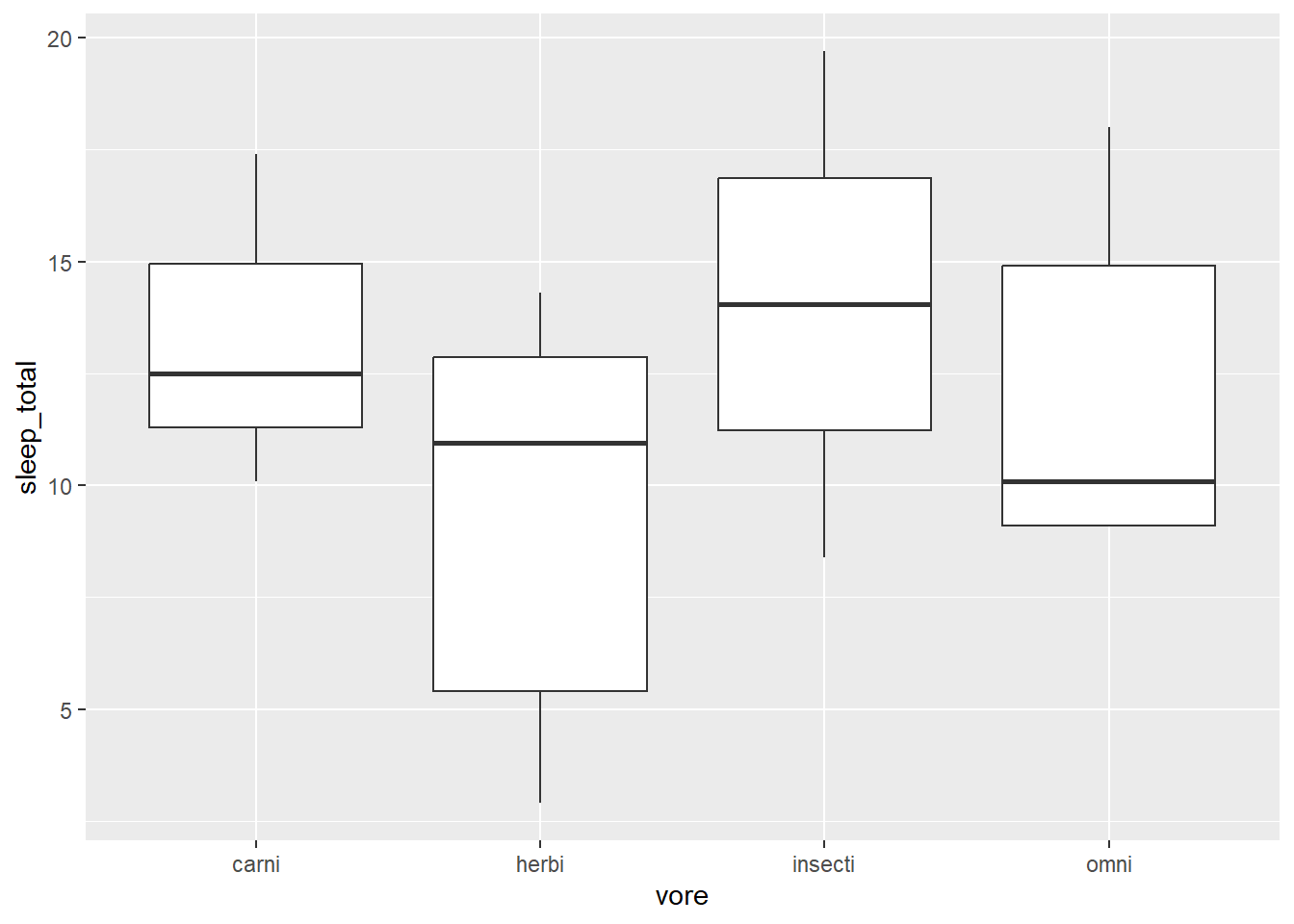
Figure 22.15: Diagramme à barre du régime alimentaire (question 8)
Question 10
- Avec le jeu de données
chickwts, produire un diagramme à barres du poids moyen des poulets par rapport à leur alimentation en ne conservant que les graines de tournesols et les fèveroles.
chickwts %>%
filter(feed %in% c("horsebean", "sunflower")) %>%
group_by(feed) %>%
summarise(poids = mean(weight)) %>%
ggplot(mapping = aes(x = feed, y = poids)) +
geom_col()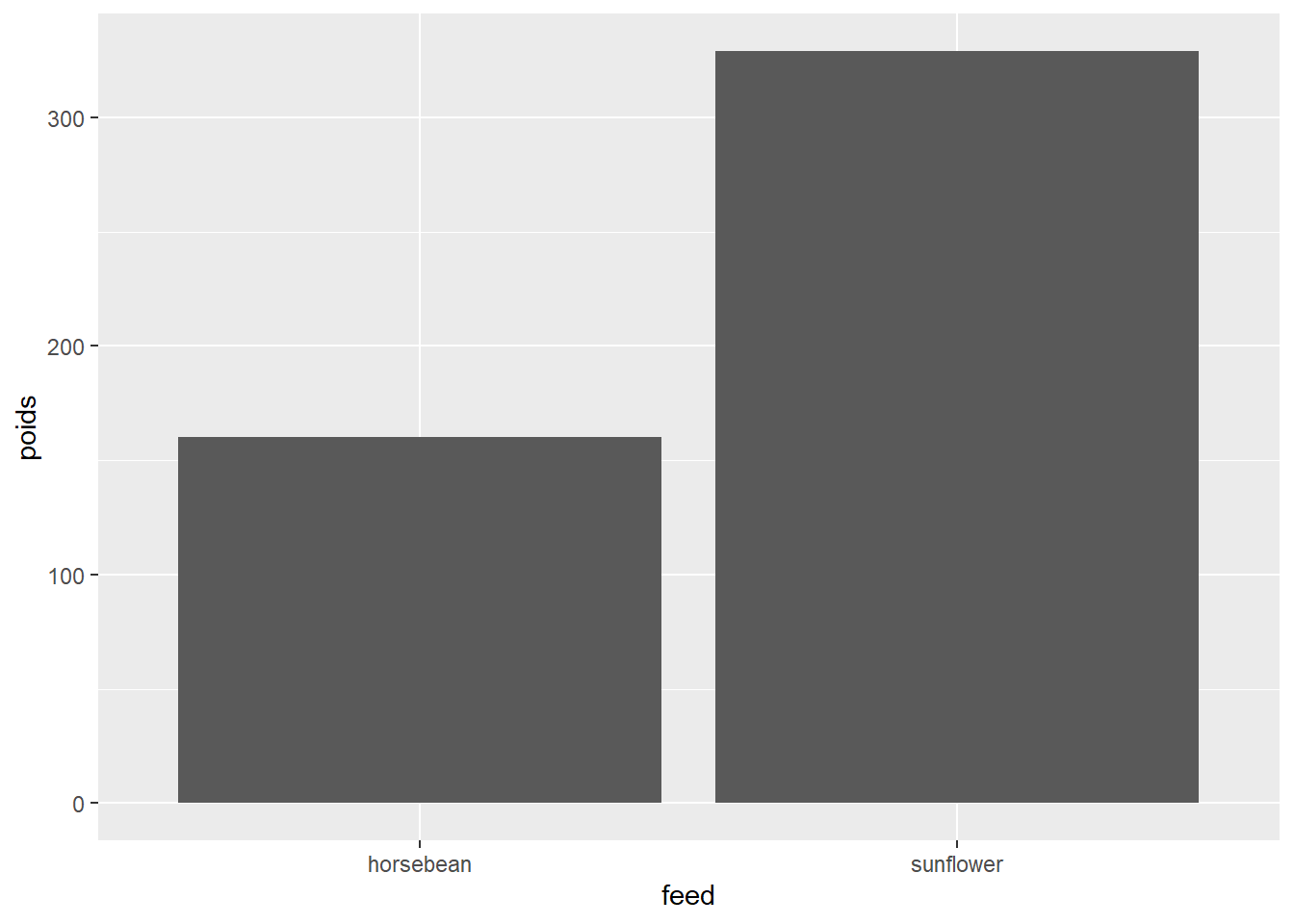
Figure 22.16: Visualiation de weight par feed (question 10)
Statistiques
Question 1
- Avec le jeu de données
mtcars, réaliser une analyse descriptive complète. Ne conservez que la moyenne, l’écart type, l’asymétrie et l’aplatissement.
psych::describe(mtcars)[c("mean","sd","skew","kurtosis")]
> mean sd skew kurtosis
> mpg 20.09 6.03 0.61 -0.37
> cyl 6.19 1.79 -0.17 -1.76
> disp 230.72 123.94 0.38 -1.21
> hp 146.69 68.56 0.73 -0.14
> drat 3.60 0.53 0.27 -0.71
> wt 3.22 0.98 0.42 -0.02
> qsec 17.85 1.79 0.37 0.34
> vs 0.44 0.50 0.24 -2.00
> am 0.41 0.50 0.36 -1.92
> gear 3.69 0.74 0.53 -1.07
> carb 2.81 1.62 1.05 1.26Voir Les variables à échelles continues pour l’utilisation de psych::describe() et Référer à des sous-éléments pour l’extraction des colonnes [c("mean","sd","skew","kurtosis")].
Question 2
- Avec le jeu de données
CO2, faire une table de contingence entreTreatmentetType.
table(CO2[c("Type","Treatment")])
> Treatment
> Type nonchilled chilled
> Quebec 21 21
> Mississippi 21 21Voir Les variables à échelles nominales pour l’utilisation de table() et Référer à des sous-éléments pour l’extraction des colonnes [c("Type","Treatment")] du jeu de données.
Question 3
- Produire les valeurs-\(t\) critiques pour \(dl = 1,2,3 ,... ,30\) et \(\alpha=.05\) unilatérale.
Question 4
- Comparer la puissance de la distribution-\(t\) avec 20 degrés de liberté par rapport à une distribution normale centrée réduite avec une \(\alpha = .05\) bilatérale. L’hypothèse alternative est distribuée normalement et fixée à une moyenne de 2 et l’écart type est de 1.
# Fixer l'alpha
alpha <- .05
# Valeurs critiques pour t et z, bilatérale (alpha/2)
# Côté supérieur avec `lower.tail = FALSE`
crit.t <- qt(alpha/2, df = 20, lower.tail = FALSE)
crit.z <- qnorm(alpha/2, lower.tail = FALSE)
# Calculer la puissance pour les deux valeurs critiques
# Fixer la moyenne à 2
pnorm(c(crit.t, crit.z), mean = 2, lower.tail = FALSE)
> [1] 0.466 0.516Question 5
- Calculer la puissance d’une corrélation de \(\rho = .30\) avec 80 participants et un \(\alpha = .05\) bilatérale. Rappel : une corrélation peut se standardiser avec la tangente hyperbolique inverse, soit
atanh(), et en multipliant par l’erreur type, \(\sqrt{n-3}\). (Question difficile)
# Fixer les paramètres
r <- .30
alpha <- .05
n <- 80
# Standardiser la corrélation
r.std <- atanh(r) * (sqrt(n-3))
#trouver la valeur critique de rejet
r.crit <- qnorm(alpha/2, lower.tail = FALSE)
#Calculer la puissance
pnorm(r.crit, mean = r.std, lower.tail = FALSE)
> [1] 0.775L’équation (11.5) de la section sur la corrélation permet de transformer ,
Question 6
- Avec le jeu de données
ToothGrowth, réaliser un test-\(t\) afin de comparer lessupppar rapport à la longueur des dents (len).
t.test(len ~ supp, data = ToothGrowth)
>
> Welch Two Sample t-test
>
> data: len by supp
> t = 2, df = 55, p-value = 0.06
> alternative hypothesis: true difference in means between group OJ and group VC is not equal to 0
> 95 percent confidence interval:
> -0.171 7.571
> sample estimates:
> mean in group OJ mean in group VC
> 20.7 17.0Question 7
- Avec le jeu de données
sleep, faire un test-\(t\) permettant de comparer les deux temps de mesure nommésgrouppar rapport à la variable dépendanteextra.
group1 <- sleep$extra[sleep$group == "1"]
group2 <- sleep$extra[sleep$group == "2"]
t.test(group1, group2, paired = TRUE)
>
> Paired t-test
>
> data: group1 and group2
> t = -4, df = 9, p-value = 0.003
> alternative hypothesis: true mean difference is not equal to 0
> 95 percent confidence interval:
> -2.46 -0.70
> sample estimates:
> mean difference
> -1.58Question 8
- Réaliser une simulation. Calculer la probabilité de gagner au jeu du roche-papier-ciseau pour chacune des options.
Plusieurs simulations sont possibles. Voici un exemple.
# Énumérer les choix
choix <- c("roche", "papier", "ciseau")
# Créer la matrice de résultats possibles
Resultats <- matrix(c(.5, 0, 1,
1, .5, 0,
0, 1, .5),
ncol = 3, nrow = 3,
byrow = TRUE,
dimnames = list(choix, choix))
# Initialiser les gains pour chaque choix
gain <- c(roche = 0, papier = 0, ciseau = 0)
# Paramètres de la u
set.seed(73)
nreps <- 10000
# La boucle
for(i in 1:nreps){
# Les joueurs des joueurs
joueur1 <- sample(choix, size = 1)
joueur2 <- sample(choix, size = 1)
# Enregistrer les gains
gain[joueur1] <- gain[joueur1] + Resultats[joueur1, joueur2]
gain[joueur2] <- gain[joueur2] + Resultats[joueur2, joueur1]
}
# Probabilités (en pourcentage)
gain / nreps
> roche papier ciseau
> 0.331 0.330 0.340Question 9
- Réaliser une simulation. Trouver la valeur critique (
c.vrit) pour un \(\alpha = .025\) unilatérale d’une distribution normale centrée sur \(0\) et un écart type de \(1/\sqrt{n}\). Le scénario : tirer aléatoirement un échantillon de \(n=30\) participants à partir d’une distribution normale de moyenne \(.5\) et un écart type de 1. Calculer la moyenne de cet échantillon. Pour chaque scénario, additionner chaque occasion où cette moyenne est plus élevée que la valeur critique. Répéter ce scénario 1000 fois. Calculer la probabilité (en pourcentage) d’occurrence selon laquelle la moyenne de l’échantillon est plus élevée que la valeur critique.
# Fixer les paramètres
alpha <- .025
n <- 30
mu1 <- .5
v.crit <- qnorm(1 - alpha, sd = 1/sqrt(n)) # ou qnorm(alpha, lower.tail = FALSE)
# Initialiser
set.seed(101)
nreps <- 1000
somme <- 0
# La boucle
for(i in 1:nreps){
# Créer un échantillon
echant <- rnorm(n = n, mean = mu1)
#Calculer la moyenne
moyenne <- mean(echant)
# Enregister si la moyenne est plus élevée que la valeur critique
somme <- somme + (moyenne >= v.crit)
}
# Probabilités (en pourcentage)
somme/nreps
> [1] 0.792Avec les renseignements précédents, calculer la puissance.
Question 10
- Réaliser un bootstrap la corrélation entre
sleep_total(temps de sommeil total) etbodywt(poids du corps) dans le jeu de donnéesmsleep(du packageggplot2). Produire la moyenne et l’écart type des échantillons bootstrapées ainsi que l’intervalle de confiance à 95%.
# Initialiser
set.seed(2018)
nreps <- 1000
N <- nrow(msleep)
alpha <- 1-.95
correl <- numeric()
# La boucle
for(i in 1:nreps){
idx <- sample(N, replace = TRUE)
D <- msleep[idx, ]
correl[i] <- cor(D$sleep_total, D$bodywt)
}
# Les statistiques
mean(correl)
> [1] -0.364
sd(correl)
> [1] 0.0694
quantile(correl, probs = c(alpha/2, 1-alpha/2))
> 2.5% 97.5%
> -0.528 -0.255Modèles linéaires
Question 1
- Avec le jeu de données
ToothGrowth, réaliser l’anova delenpar rapport à l’interaction entresuppetdose. Consulter le sommaire.
res.aov <- aov(len ~ supp * dose, data = ToothGrowth)
summary(res.aov)
> Df Sum Sq Mean Sq F value Pr(>F)
> supp 1 205 205 12.32 0.00089 ***
> dose 1 2224 2224 133.42 < 2e-16 ***
> supp:dose 1 89 89 5.33 0.02463 *
> Residuals 56 934 17
> ---
> Signif. codes:
> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Question 2
- Avec le jeu de données
ToothGrowth, réaliser le régression delenpar rapport à l’interaction entresuppetdose. Consulter le sommaire.
res.lm <- lm(len ~ supp * dose, data = ToothGrowth)
summary(res.lm)
>
> Call:
> lm(formula = len ~ supp * dose, data = ToothGrowth)
>
> Residuals:
> Min 1Q Median 3Q Max
> -8.23 -2.85 0.05 2.29 7.94
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 11.55 1.58 7.30 1.1e-09 ***
> suppVC -8.26 2.24 -3.69 0.00051 ***
> dose 7.81 1.20 6.53 2.0e-08 ***
> suppVC:dose 3.90 1.69 2.31 0.02463 *
> ---
> Signif. codes:
> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
> Residual standard error: 4.08 on 56 degrees of freedom
> Multiple R-squared: 0.73, Adjusted R-squared: 0.715
> F-statistic: 50.4 on 3 and 56 DF, p-value: 6.52e-16Question 3
- Créer un jeu de données pour la structure de la Figure 17.7. Le jeu de données est standardisé et contient 123 sujets.
n <- 123
set.seed(n)
x <- rnorm(n)
y <- .5 * x + sqrt(1-.5^2) * rnorm(n)
z <- .5 * y + sqrt(1-.5^2) * rnorm(n)
jd <- data.frame(x = x, y = y, z = z)
head(jd)
> x y z
> 1 -0.5605 -0.5020 -0.338
> 2 -0.2302 1.4817 -0.437
> 3 1.5587 0.2147 -0.468
> 4 0.0705 0.2391 0.540
> 5 0.1293 0.1322 -0.259
> 6 1.7151 0.0245 -0.474Question 4
- Créer un jeu de données pour la structure de la Figure 17.8. Le jeu de données est standardisé et contient 456 sujets.
n <- 456
set.seed(n)
q <- rnorm(n)
w <- .7 * q + sqrt(1-(.7)^2) * rnorm(n)
r <- -.7 * w + sqrt(1-(-.7)^2) * rnorm(n)
e <- -.8 * q + sqrt(1-(-.8)^2) * rnorm(n)
y <- .8 * e + sqrt(1-(.8)^2) * rnorm(n)
jd <- data.frame(q = q, w = w, e = e, r = r,y = y)
head(jd)
> q w e r y
> 1 -1.344 -0.591 0.849 0.6451 0.9648
> 2 0.622 0.344 -0.404 -0.1897 -0.0720
> 3 0.801 0.949 0.147 -0.9513 -1.1297
> 4 -1.389 -0.913 2.880 1.2526 1.8879
> 5 -0.714 0.121 0.255 0.0432 -0.3850
> 6 -0.324 1.922 0.518 -1.7115 0.0752Question 5
- Créer un jeu de données pour la structure de la Figure 17.9. Le jeu de données est standardisé et contient 789 sujets.
Pour faciliter la résolution de cette quesiton, il est beaucoup plus simplede passer par le [Cas général] de génération de données et d’utiliser la fonction maison beta2cov qui s’importe en collant la syntaxe directement dans l’environnement R ou qui est disponible dans le package pathanalysis vu dans la section Rapporter l’analyse de médiation.
library(pathanalysis)
n <- 789
set.seed(n)
# Créer de la matrice de coefficients de régression
B <- matrix(c(0, 0, 0, 0,
.3, 0, 0, 0,
-.3, 0, 0, 0,
.1, .4,-.4, 0),
ncol = 4, nrow = 4,
byrow = TRUE,
dimnames = list(c("x", "y", "w", "z"),
c("x", "y", "w", "z")))
# L'argument `dimnames` ne sert qu'à nommer les dimensions
# Produire la matrice de covariance à partir de la matrice Beta
S <- beta2cov(B)
# Générer les données
jd <- MASS::mvrnorm(n = n,
mu = rep(0, ncol(S)),
Sigma = S)
head(jd)
> x y w z
> [1,] 0.869 0.728 0.0987 0.0627
> [2,] -3.291 -0.738 0.7189 -1.6190
> [3,] 0.790 -1.245 -0.7083 -0.2671
> [4,] -0.347 1.254 0.0845 -0.1919
> [5,] 0.280 -0.521 0.7192 -0.1251
> [6,] -0.819 -0.867 0.1130 0.2644Question 6
- Avec le jeu de données de la Question 5, réaliser l’analyse de médiation.
Il existe plusieurs façona de faire l’analyse de l’analyse de médiation. Voici celle avec la fonction mediation() du package pathanalysis.
# Vérifier que les variables ont bien des nom de colonnes
# Pour s'en assurer
# colnames(jd) <- c("x", "y", "w", "z")
# La fonction `mediation()` du package `pathanalysis`
mediation(z ~ w ~ y ~ x, data = jd, standardized = TRUE)
> Estimate S.E. CI Lower 95 %
> x -> y 0.312 0.036 0.243
> x -> w -0.325 0.037 -0.399
> x -> z 0.120 0.030 0.060
> y -> w 0.018 0.035 -0.049
> y -> z 0.402 0.028 0.349
> w -> z -0.368 0.028 -0.420
> x -> y -> w 0.006 0.011 -0.016
> x -> y -> z 0.125 0.017 0.095
> x -> w -> z 0.120 0.016 0.089
> y -> w -> z -0.007 0.013 -0.032
> x -> y -> w -> z -0.002 0.004 -0.010
> total indirect x -> z 0.243 0.023 0.200
> total effect x -> z 0.363 0.034 0.294
> CI Upper 95 % p-value
> x -> y 0.383 0.000
> x -> w -0.252 0.000
> x -> z 0.179 0.000
> y -> w 0.088 0.603
> y -> z 0.457 0.000
> w -> z -0.313 0.000
> x -> y -> w 0.027 0.608
> x -> y -> z 0.160 0.000
> x -> w -> z 0.153 0.000
> y -> w -> z 0.019 0.603
> x -> y -> w -> z 0.006 0.607
> total indirect x -> z 0.289 0.000
> total effect x -> z 0.430 0.000Question 7
- Avec le jeu de données
ToothGrowth, analyser l’interaction entresuppetdosesur la variable dépendantelen. Produire les graphiques
res.lm <- lm(len ~ supp * dose, data = ToothGrowth)
summary(res.lm)
>
> Call:
> lm(formula = len ~ supp * dose, data = ToothGrowth)
>
> Residuals:
> Min 1Q Median 3Q Max
> -8.23 -2.85 0.05 2.29 7.94
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 11.55 1.58 7.30 1.1e-09 ***
> suppVC -8.26 2.24 -3.69 0.00051 ***
> dose 7.81 1.20 6.53 2.0e-08 ***
> suppVC:dose 3.90 1.69 2.31 0.02463 *
> ---
> Signif. codes:
> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
> Residual standard error: 4.08 on 56 degrees of freedom
> Multiple R-squared: 0.73, Adjusted R-squared: 0.715
> F-statistic: 50.4 on 3 and 56 DF, p-value: 6.52e-16Le graphique des pentes simples.
library(interactions)
interact_plot(model = res.lm,
pred = dose,
modx = supp)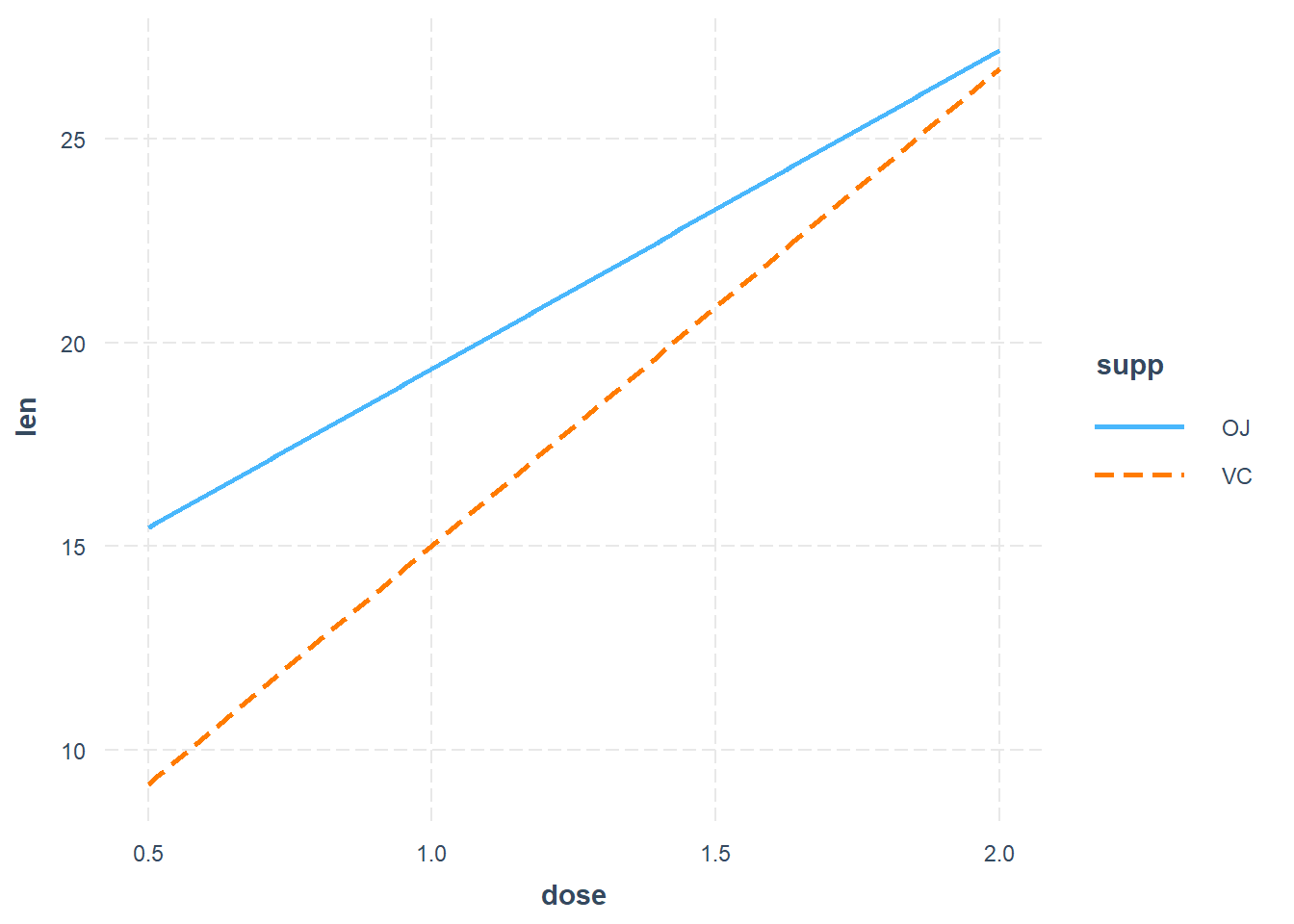
Figure 22.17: Le graphique des pentes simples (question 7)
Le graphique de Johnson-Neyman.
sim_slopes(model = res.lm,
pred = dose,
modx = supp,
jnplot = TRUE)
> Warning: Johnson-Neyman intervals are not available for factor
> predictors or moderators.
> SIMPLE SLOPES ANALYSIS
>
> Slope of dose when supp = OJ:
>
> Est. S.E. t val. p
> ------ ------ -------- ------
> 7.81 1.20 6.53 0.00
>
> Slope of dose when supp = VC:
>
> Est. S.E. t val. p
> ------- ------ -------- ------
> 11.72 1.20 9.80 0.00Analyses factorielles
Question 1
- Créer un jeu de données pour la structure de la Figure 20.9. Le jeu de données est standardisé et contient 584 sujets.
# Programmer la structure factorielle
FS <- matrix(c(.5, .5, .3, .2, 0, 0, 0, 0, 0,
0, 0, 0, .7, .7, .7, 0, 0, 0,
0, 0, 0, 0, 0, .2, .3, .4, .3),
ncol = 3, nrow = 9,
dimnames = list(paste0("i",1:9),
paste0("F",1:3)))
# L'argument `dimnames` ne sert qu'à nommer les dimensions
# Transformer ne matrice de corrélation
R <- FS %*% t(FS)
# Ajouter le bruit dans la diagonale
diag(R) <- 1
# Générer le jeu de données
set.seed(584)
jd <- MASS::mvrnorm(n = 584,
mu = rep(0, ncol(R)),
Sigma = R)
# Voici les premières données.
head(jd)
> i1 i2 i3 i4 i5 i6 i7 i8
> [1,] 0.489 0.666 0.936 -0.263 -1.416 -0.565 -0.327 0.573
> [2,] 2.251 1.601 0.563 0.636 0.443 0.998 -0.409 -1.050
> [3,] 0.917 2.349 0.644 0.232 1.472 0.506 1.550 -0.374
> [4,] 0.054 -0.583 0.544 0.518 1.418 0.849 -1.497 0.249
> [5,] 0.428 -1.409 -0.319 1.803 0.800 0.584 1.459 -1.496
> [6,] 0.122 0.459 -0.524 -0.665 -0.675 -0.393 0.395 -0.121
> i9
> [1,] -0.0283
> [2,] -0.0520
> [3,] -0.5925
> [4,] -0.4915
> [5,] -0.3259
> [6,] 0.1591Question 2
- Utiliser la fonction
eigen()pour extraire les valeurs propres, la variance expliquée de chacune d’elle et les loadings du jeu de données de la Question 1.
# L'analyse en composantes principales
res.acp <- eigen(cor(jd))
# Les valeurs propres
res.acp$values
> [1] 1.986 1.367 1.250 0.984 0.897 0.785 0.761 0.503 0.468
# Leur variance expliquée
res.acp$values / ncol(jd)
> [1] 0.2206 0.1518 0.1389 0.1094 0.0996 0.0872 0.0846 0.0559
> [9] 0.0520
# Les loadings (pour toutes les dimensions)
res.acp$vectors %*% diag(sqrt(res.acp$values))
> [,1] [,2] [,3] [,4] [,5] [,6]
> [1,] 0.15072 0.6776 0.1101 0.10901 -0.16094 0.6295
> [2,] 0.13596 0.5962 0.2087 -0.47882 0.09149 -0.0687
> [3,] 0.13756 0.6536 0.0685 0.37469 -0.00409 -0.5843
> [4,] 0.83004 -0.0229 0.0341 -0.04461 -0.02579 -0.0199
> [5,] 0.79778 -0.1475 0.1708 -0.00734 0.01265 -0.0669
> [6,] 0.77087 -0.2000 -0.1981 0.05133 -0.02211 0.0780
> [7,] 0.03508 0.1477 -0.5661 -0.67715 0.08179 -0.1098
> [8,] 0.00983 0.1087 -0.6674 0.16089 -0.64746 -0.0442
> [9,] 0.06704 0.1702 -0.5951 0.33729 0.65972 0.1328
> [,7] [,8] [,9]
> [1,] -0.2625 0.00133 0.05561
> [2,] 0.5825 -0.02710 0.01007
> [3,] -0.2361 -0.10055 0.03887
> [4,] -0.0722 0.12182 -0.53501
> [5,] -0.0214 0.39869 0.38539
> [6,] 0.0907 -0.53358 0.15615
> [7,] -0.4191 0.00327 0.05981
> [8,] 0.2760 0.13924 0.00353
> [9,] 0.1772 0.11894 -0.01461Question 3
- Créer une fonction maison pour le test de Kaiser et utiliser le jeu de données créé à la Question 1.
Question 4
- Créer une fonction maison pour l’analyse parallèle et utiliser le jeu de données créé à la Question 1.
parallel.maison <- function(eig, ns, nreps = 1000, percentile = .5){
# Répliquer (replicate) l'ACP (eigen) d'une matrice
# de corrélation (cor) de données aléatoires (rnorm)
S.eig <- replicate(n = nreps,
eigen(cor(matrix(rnorm(length(eig)*ns),
ncol = length(eig))))$values)
crit <- apply(X = S.eig,
FUN = quantile,
MARGIN = 1,
probs = percentile)
return(min(which(eig < crit)) - 1)
}
parallel.maison(res.acp$values, ns = 584)
> [1] 3Question 5
- Utiliser
Rnestavec le jeu de données créé à la Question 1. Produire une graphique.
library(Rnest)
FALSE
FALSE Attachement du package : 'Rnest'
FALSE L'objet suivant est masqué depuis 'package:tidyr':
FALSE
FALSE nest
FALSE L'objet suivant est masqué depuis 'package:stats':
FALSE
FALSE loadings
res <- nest(jd)
res
FALSE At 95% confidence, Next Eigenvalue Sufficiency Test (NEST) suggests 3 factors.
plot(res)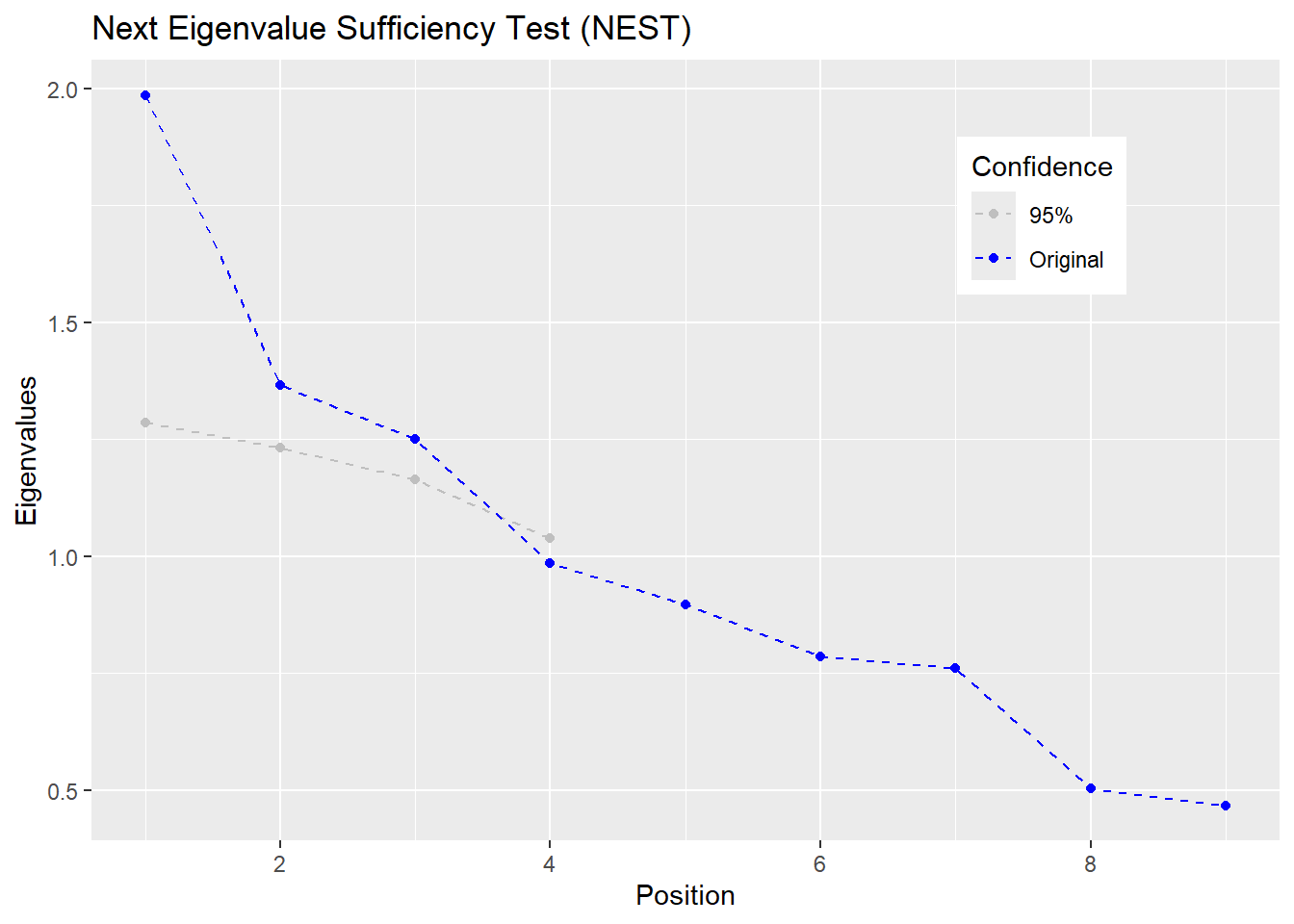
Question 6
- Utiliser
factanal()pour 3 facteurs avec le jeu de données créé à la Question 1. Extraire les scores et les loadings.
# L'analyse factorielle
res.fa <- factanal(jd,
factors = 3,
scores = "regression")
res.fa
>
> Call:
> factanal(x = jd, factors = 3, scores = "regression")
>
> Uniquenesses:
> i1 i2 i3 i4 i5 i6 i7 i8 i9
> 0.770 0.857 0.812 0.471 0.454 0.463 0.938 0.837 0.892
>
> Loadings:
> Factor1 Factor2 Factor3
> i1 0.474
> i2 0.375
> i3 0.430
> i4 0.711 0.153
> i5 0.716 -0.173
> i6 0.691 0.229
> i7 0.247
> i8 0.403
> i9 0.326
>
> Factor1 Factor2 Factor3
> SS loadings 1.498 0.586 0.421
> Proportion Var 0.166 0.065 0.047
> Cumulative Var 0.166 0.232 0.278
>
> Test of the hypothesis that 3 factors are sufficient.
> The chi square statistic is 14.1 on 12 degrees of freedom.
> The p-value is 0.292
# Extraire les scores
res.fa$scores
> Factor1 Factor2 Factor3
> [1,] -0.83366 0.58358 0.342690
> [2,] 0.76889 1.24111 -0.160501
> [3,] 0.85308 1.05470 -0.275355
> [4,] 1.08709 -0.07155 -0.411387
> [5,] 1.21651 -0.14465 -0.325073
> [6,] -0.59656 -0.08773 0.072458
> [7,] -0.54468 -0.61439 -1.637814
> [8,] -0.05967 0.26519 0.023142
> [9,] 0.66283 -0.60101 0.959725
> [10,] -0.10487 0.13781 -1.332906
> [11,] -0.05522 -0.39171 0.514765
> [12,] 1.82187 0.67113 0.341810
> [13,] 0.01411 0.73428 -1.156857
> [14,] 0.21964 0.98978 0.380414
> [15,] 0.32852 0.63906 0.356436
> [16,] 0.35250 0.40031 -0.515344
> [17,] -0.09693 0.08499 -0.340046
> [18,] 0.21520 -0.60417 0.230251
> [19,] -1.29674 -0.77926 -0.055553
> [20,] 2.50988 0.20077 0.995164
> [21,] -0.17189 1.28995 -0.195673
> [22,] 1.08950 -0.37615 0.207520
> [23,] 0.66918 0.86039 0.271027
> [24,] -1.53354 0.09630 0.245623
> [25,] 0.10844 0.28343 0.704891
> [26,] 0.93994 0.21780 0.572182
> [27,] 1.49451 -1.00048 -0.057803
> [28,] 0.32748 2.11153 -0.003385
> [29,] 0.16111 -1.35284 0.278450
> [30,] 0.51204 -0.50717 0.428596
> [31,] -0.14014 0.14923 -1.258340
> [32,] -0.95141 -0.25945 0.571332
> [33,] 0.42996 0.00156 -0.182604
> [34,] 0.08602 -0.80171 -0.805013
> [35,] 0.69506 -0.31801 0.083405
> [36,] -0.42497 -0.37251 0.090079
> [37,] 1.29473 1.30164 0.825328
> [38,] 1.05747 1.19074 -0.984881
> [39,] 0.23639 -0.29245 0.661033
> [40,] 0.35086 -0.57473 -0.779951
> [41,] 0.33842 -0.97260 0.422997
> [42,] 0.55561 -0.27252 -0.701154
> [43,] -0.23122 0.09536 -0.684730
> [44,] -0.56670 0.15954 0.419495
> [45,] 1.99893 0.50315 -0.346903
> [46,] -0.81484 1.15375 0.047917
> [47,] -0.41105 -0.83073 -0.435116
> [48,] -1.03249 -1.29206 0.173158
> [49,] 0.95858 -0.69215 -0.343312
> [50,] 0.32455 0.46564 -0.601205
> [51,] 0.08558 -0.38999 -0.844208
> [52,] 0.99142 0.00887 1.270202
> [53,] 1.32885 1.07354 0.556514
> [54,] 0.03630 0.96568 -0.284066
> [55,] -1.44638 0.35967 -0.863391
> [56,] -0.23090 -0.14944 1.379261
> [57,] -0.46146 1.14282 1.495109
> [58,] 0.53671 -0.92566 0.451991
> [59,] 0.53974 1.29301 0.114702
> [60,] 0.00922 0.15783 -0.107781
> [61,] 0.34033 0.60310 0.425249
> [62,] -2.13393 0.26909 0.230915
> [63,] -0.29221 -0.69697 -0.277423
> [64,] 0.03429 0.03258 -0.857771
> [65,] 0.99198 0.19662 -0.723475
> [66,] 1.05837 0.28110 0.699938
> [67,] 1.47163 0.27783 -0.100761
> [68,] 0.29715 0.38838 -0.491096
> [69,] -0.74657 0.12301 -0.445042
> [70,] 0.60748 0.72057 0.588835
> [71,] -2.35699 0.22659 0.122496
> [72,] -1.45939 0.53260 0.196858
> [73,] 0.04597 -0.12751 -0.309984
> [74,] 0.47292 0.38336 -0.667654
> [75,] 0.35212 -0.77788 -0.274501
> [76,] -0.50230 0.45790 -0.413664
> [77,] 0.24104 -0.57589 0.413615
> [78,] 0.53554 0.24366 0.018391
> [79,] 0.09826 -0.85608 0.478283
> [80,] -0.43518 0.26106 -0.368034
> [81,] 0.29795 -0.30960 0.992972
> [82,] 0.89006 -0.44839 -0.081774
> [83,] 0.78428 0.98966 0.175311
> [84,] -0.31630 0.47048 -1.100788
> [85,] 0.62419 0.54838 -0.187761
> [86,] -0.33409 -0.65235 -1.271664
> [87,] 0.12075 -0.90995 -0.353222
> [88,] 0.67489 0.21985 0.405949
> [89,] 0.02559 0.49581 0.839946
> [90,] -0.93627 -0.06853 0.403047
> [91,] -0.46991 -0.22387 0.031650
> [92,] -0.39500 0.38507 -0.786081
> [93,] -1.53854 -0.62229 1.246333
> [94,] 0.58009 0.64814 0.882283
> [95,] -1.73038 0.79093 0.066325
> [96,] -0.18242 -0.00889 0.263813
> [97,] -0.46408 0.52134 0.200910
> [98,] 0.08985 -0.35297 0.565880
> [99,] 0.55612 -0.91685 0.000405
> [100,] 0.30679 0.46088 -0.474611
> [101,] -0.31214 0.83368 0.050967
> [102,] 1.00147 -1.10772 -1.090463
> [103,] -0.21593 0.06259 0.817170
> [104,] -0.03331 0.08437 -0.233618
> [105,] 0.08788 -0.07796 0.705683
> [106,] -1.13227 0.64975 0.136063
> [107,] -0.54390 -1.03458 -0.661280
> [108,] 0.49542 -0.03883 -0.585572
> [109,] 0.83970 0.35965 -1.010159
> [110,] 0.46492 1.10603 -0.685535
> [111,] -1.18779 -0.85958 -1.308114
> [112,] 0.28693 0.67686 -0.610832
> [113,] -0.91179 0.06728 0.189939
> [114,] 0.27856 -0.61626 0.214894
> [115,] -0.25920 0.59118 -0.198770
> [116,] 0.05791 -1.21397 0.641136
> [117,] 0.64682 0.35335 0.217462
> [118,] 1.27781 0.38729 0.302326
> [119,] -1.00092 0.46925 0.238805
> [120,] -1.53262 -0.22758 -1.394575
> [121,] -0.49455 0.17226 0.930756
> [122,] -0.84313 -0.37568 0.058610
> [123,] -0.11659 0.21998 0.810858
> [124,] -0.87496 -0.83672 0.422494
> [125,] 1.33830 -0.26177 -0.952818
> [126,] 1.05112 1.39875 -0.042975
> [127,] 0.55216 -0.61576 -0.959522
> [128,] 0.20487 -1.04833 -0.037500
> [129,] -0.57603 -0.80214 -0.032636
> [130,] -1.24724 0.22529 -0.155338
> [131,] 0.67515 1.09492 -0.815557
> [132,] 2.01186 -0.42069 0.078669
> [133,] -0.31607 0.50831 0.057357
> [134,] -0.47495 0.16986 -0.210380
> [135,] -0.04391 -0.48351 -0.445600
> [136,] 0.49134 -0.81502 0.254078
> [137,] 0.01861 -0.58322 -0.301274
> [138,] 0.14252 0.97910 -0.655383
> [139,] 0.24322 1.03970 -0.264538
> [140,] -0.09103 0.09800 0.606684
> [141,] 2.03356 0.32586 -0.002490
> [142,] 0.28390 0.45164 -0.850906
> [143,] -0.61878 0.07582 0.758275
> [144,] 0.81753 -0.72803 0.067334
> [145,] 1.06914 -0.97552 -1.052529
> [146,] -0.99072 -0.84321 1.544579
> [147,] -0.64774 -0.15631 0.044261
> [148,] 1.41346 0.28984 0.512343
> [149,] 0.25114 0.70591 0.759327
> [150,] 0.14466 -0.21989 0.280057
> [151,] -1.13382 -0.10123 0.451275
> [152,] 0.62669 -0.18528 0.820711
> [153,] 0.33358 -0.47331 0.375185
> [154,] 1.10418 0.40144 0.464436
> [155,] -0.01503 -0.32293 0.480190
> [156,] 0.13541 0.72843 -0.614199
> [157,] -0.30304 1.21617 -0.881363
> [158,] -1.14589 -0.60295 -0.013967
> [159,] -0.57276 0.22088 0.189424
> [160,] -0.85703 0.47614 -0.578018
> [161,] 0.30496 -0.50849 0.354217
> [162,] -0.94122 0.23123 -0.474627
> [163,] 0.49690 -1.07692 -0.112242
> [164,] -0.44492 0.77375 -1.005674
> [165,] -0.03189 -0.11696 0.637828
> [166,] -0.40257 0.13072 -0.138532
> [167,] -2.29408 -0.23693 -0.049400
> [168,] 0.81532 0.85180 0.097546
> [169,] 0.87669 -0.63879 -0.164307
> [170,] -0.11192 -0.42086 0.589782
> [171,] 1.82450 -0.52647 -0.879305
> [172,] 1.15915 0.07141 0.395764
> [173,] 0.73654 0.82785 -0.321302
> [174,] 1.12141 -0.26747 -0.170157
> [175,] 0.39953 1.08186 -0.022477
> [176,] -0.48312 -0.20080 -0.720880
> [177,] -0.32087 -0.20092 -1.157097
> [178,] -1.29264 -0.41486 0.254806
> [179,] -0.28013 -0.59272 -1.181823
> [180,] -0.59174 0.19740 -0.336245
> [181,] 2.47811 -0.02575 -0.107795
> [182,] -0.36513 -0.05887 -0.373211
> [183,] 0.50823 -0.91799 0.434710
> [184,] -0.25993 0.08851 0.807036
> [185,] 0.03759 0.29855 0.113889
> [186,] -0.70216 1.05667 -0.886259
> [187,] 0.57100 -0.04014 0.110798
> [188,] -0.22546 0.94019 0.735268
> [189,] 0.10265 -0.12756 -0.029189
> [190,] 0.10629 0.56707 -0.357094
> [191,] -2.01336 -0.50733 -0.163194
> [192,] 1.45509 0.51868 0.442138
> [193,] 0.64089 0.96288 0.383998
> [194,] 0.14558 0.56946 -0.029618
> [195,] -0.23784 -1.28682 0.049096
> [196,] -1.08102 0.73301 -0.816188
> [197,] 0.21298 0.14085 0.627924
> [198,] -0.47199 -0.00102 0.326666
> [199,] -0.26779 -1.21933 1.129719
> [200,] -0.41982 -0.09976 0.009351
> [201,] -2.15012 0.22385 -0.479056
> [202,] 0.55725 -0.20260 0.001828
> [203,] -0.87193 -0.20890 0.549921
> [204,] 0.16389 0.74865 -0.579059
> [205,] -0.14271 1.81682 -0.037279
> [206,] -0.10104 1.26200 -0.272604
> [207,] -1.26246 -0.98870 -0.664690
> [208,] -0.83550 -0.15402 0.050639
> [209,] 0.10350 -0.78933 -0.286576
> [210,] -0.08393 -1.23916 -0.292363
> [211,] -0.11262 0.18532 1.177732
> [212,] 0.87216 -0.12151 0.849816
> [213,] -0.21997 -1.11834 -0.586156
> [214,] 0.04472 -0.05484 0.931295
> [215,] 0.19396 0.62020 0.578771
> [216,] 0.21466 0.24257 -0.450137
> [217,] 0.32608 0.28378 0.147317
> [218,] 0.27308 0.97399 0.702685
> [219,] -0.07387 0.35214 0.688794
> [220,] 0.54810 -0.61060 -0.004821
> [221,] -0.36846 -0.37162 0.652137
> [222,] 0.95125 0.11810 -0.265583
> [223,] 1.12915 0.39455 -0.115776
> [224,] -0.00856 0.37348 -0.881770
> [225,] -1.77611 -0.78168 -0.498161
> [226,] 0.47873 -0.37026 -0.035027
> [227,] 0.13516 0.33211 -0.838501
> [228,] -0.25566 0.39385 -0.746493
> [229,] 0.47185 -0.70742 0.959659
> [230,] -1.42803 0.46587 -0.081241
> [231,] 1.00035 0.65148 -0.170668
> [232,] -0.40474 0.38414 -0.901872
> [233,] 0.19063 0.51127 0.330418
> [234,] -0.27645 -0.85877 0.874765
> [235,] -0.53454 -0.14826 0.142216
> [236,] -0.39758 0.19231 -0.081596
> [237,] 1.19157 0.69093 1.004801
> [238,] 1.73616 0.29029 0.619564
> [239,] -0.21639 0.54620 0.202189
> [240,] -0.33191 -1.25322 0.109755
> [241,] 0.15401 1.40200 0.421219
> [242,] -0.79634 -0.42680 -0.191401
> [243,] 0.77839 -0.13347 -0.184682
> [244,] 0.70725 -0.56492 -0.582056
> [245,] -0.93920 -0.62830 0.282492
> [246,] -0.01252 -1.05019 -0.573996
> [247,] -0.44232 -0.62773 -0.047710
> [248,] 0.22532 -0.12492 0.592077
> [249,] -1.21788 0.74633 -0.236966
> [250,] 0.71104 -0.48661 0.185759
> [251,] -0.82800 -0.02291 -1.198462
> [252,] -1.05657 -0.33134 0.336086
> [253,] -0.39066 0.83283 -0.732931
> [254,] 0.17967 0.30150 -0.051138
> [255,] 0.42566 -0.42791 -0.792029
> [256,] 1.47302 -0.83453 -0.320927
> [257,] 0.42161 1.55125 -0.823539
> [258,] -0.17556 -0.10135 0.323337
> [259,] -0.91810 0.50169 1.564949
> [260,] 0.07449 0.83637 -0.102961
> [261,] -0.27475 0.70066 0.647827
> [262,] -1.06450 -0.16954 -0.087521
> [263,] 1.87548 -0.20394 -1.204906
> [264,] -1.16747 0.12721 -0.431845
> [265,] -0.86187 0.57930 -0.024474
> [266,] 0.47824 -1.01323 -0.046878
> [267,] 0.56925 -0.15182 0.850935
> [268,] -0.96625 -0.49698 0.621760
> [269,] -0.23909 -0.47457 -0.225663
> [270,] 0.45427 -0.07726 0.347640
> [271,] -0.12909 -0.38269 0.950243
> [272,] -2.31486 -0.91144 -0.498224
> [273,] 0.95038 -0.05397 -0.047770
> [274,] -0.32135 -0.46166 -0.236173
> [275,] -0.10237 0.35625 0.321577
> [276,] -0.62043 -0.27629 -0.375142
> [277,] -1.54561 -0.35520 -1.141906
> [278,] -0.37093 -0.55419 -0.102723
> [279,] 1.28305 0.66901 -0.429401
> [280,] 1.24162 0.15291 -0.409985
> [281,] -0.11610 0.93966 -0.928237
> [282,] -0.51709 -0.08019 -0.672568
> [283,] -1.27537 1.15566 0.323371
> [284,] -0.61706 0.01361 -0.349877
> [285,] 0.52371 0.56001 -0.311415
> [286,] 0.32707 -0.66088 -0.895286
> [287,] 0.56562 0.39212 0.440564
> [288,] -1.70364 -0.77350 0.575336
> [289,] -0.50237 -1.20729 0.471056
> [290,] 1.41713 0.95548 0.750766
> [291,] 1.54177 1.43574 -0.617593
> [292,] 0.05538 -0.25872 -0.370460
> [293,] 0.89863 -0.77283 0.145793
> [294,] -1.10537 -1.24092 0.767918
> [295,] 0.50774 0.04623 0.106541
> [296,] 0.29393 0.15282 -0.311169
> [297,] -0.29032 0.27915 -0.135805
> [298,] -0.37559 -0.16338 1.002318
> [299,] 0.38439 0.97709 0.073120
> [300,] -0.79387 -0.77624 -0.264213
> [301,] -0.53111 -0.80262 -0.196966
> [302,] -0.77401 -0.13737 0.697164
> [303,] 2.29525 -0.04093 -1.016569
> [304,] 0.84927 -0.46442 0.360956
> [305,] 0.68281 0.25092 0.381776
> [306,] 1.86410 1.20398 -0.129118
> [307,] 0.60200 -0.81176 -0.275922
> [308,] -0.13185 -0.71211 0.445464
> [309,] -0.46913 0.30024 0.030282
> [310,] -2.00381 -0.24868 -1.022072
> [311,] 1.57091 -0.27040 0.201151
> [312,] -0.28238 0.31986 0.328192
> [313,] 0.42629 -0.75019 -0.056034
> [314,] -0.68479 -0.05159 0.200631
> [315,] -0.90255 -1.17194 -0.221483
> [316,] 0.04894 -0.21845 0.699941
> [317,] -0.34604 -0.78084 -0.498391
> [318,] 0.51178 -0.05501 0.200101
> [319,] 0.09529 1.41423 -1.382712
> [320,] 0.33555 0.25549 -0.022258
> [321,] 0.59167 1.35870 0.412462
> [322,] 1.09530 -0.87092 -0.338222
> [323,] -1.94962 0.23914 -0.605945
> [324,] -0.90414 0.36988 -0.938254
> [325,] -0.95494 -0.79750 0.108207
> [326,] 0.96172 -1.13319 0.937566
> [327,] 0.30438 -0.12261 -0.054201
> [328,] 0.73068 -1.21731 -1.212104
> [329,] -1.84049 -0.06647 0.712258
> [330,] 0.42551 -0.23563 -1.223503
> [331,] 1.47277 0.20502 1.052293
> [332,] -0.75907 0.96233 1.085536
> [333,] -1.21375 1.21865 0.631939
> [334,] -0.90839 0.35460 0.783609
> [335,] -0.75533 0.01179 0.076865
> [336,] -0.80705 0.25524 -0.080266
> [337,] 1.20456 -0.80241 -0.007428
> [338,] -0.39301 -0.12431 -0.521390
> [339,] 0.09858 0.75171 0.250673
> [340,] 0.05565 0.89017 -0.044932
> [341,] -1.37632 0.62437 0.351195
> [342,] -0.71669 0.79623 -0.442349
> [343,] -0.51330 0.30929 0.519968
> [344,] -0.50818 -0.65325 -0.210873
> [345,] 0.22201 -0.08255 -0.568643
> [346,] 0.79863 -0.01926 0.296055
> [347,] -0.75165 -0.41656 -1.045483
> [348,] -0.44083 0.34060 -0.211199
> [349,] 1.06070 0.62224 -0.666412
> [350,] 0.17606 -0.15952 -0.399415
> [351,] 1.65637 -0.28332 0.358025
> [352,] 0.25145 -0.61578 -0.264908
> [353,] -1.10266 -0.04530 0.481103
> [354,] 0.41340 -0.85969 -0.513597
> [355,] -0.21130 -0.31045 -0.285809
> [356,] 0.06969 -0.75547 0.436153
> [357,] 0.63839 -0.06172 0.232435
> [358,] -0.46479 0.53129 -0.084766
> [359,] -1.01281 0.07389 -0.950152
> [360,] 0.29616 0.33670 -0.096206
> [361,] 1.47887 -0.00321 1.343584
> [362,] 0.10095 -0.75951 -1.046935
> [363,] -0.05194 0.28141 -0.463767
> [364,] -0.83998 0.47878 0.621333
> [365,] 0.71411 -0.67768 0.436926
> [366,] -0.04245 -0.68972 -0.371779
> [367,] 0.05277 -0.31389 0.285059
> [368,] 0.14082 0.24758 0.356710
> [369,] 0.57168 -1.37316 0.399063
> [370,] -0.60132 0.21719 0.334246
> [371,] -0.27803 -1.01832 1.075438
> [372,] -1.53384 -0.09292 -0.431847
> [373,] 0.71200 0.43113 -0.357880
> [374,] 0.60573 0.14440 -0.374983
> [375,] -0.87308 0.07889 -0.096816
> [376,] -0.01215 1.33557 0.646193
> [377,] 0.87327 -0.29874 0.427905
> [378,] -1.13997 -0.12785 -0.366527
> [379,] 0.85276 0.38835 -0.125325
> [380,] -0.29928 -0.09350 -0.324652
> [381,] -0.77589 0.35805 0.386553
> [382,] 0.40013 0.73075 1.242977
> [383,] 0.01393 0.15633 0.114755
> [384,] -0.78309 1.41191 1.148545
> [385,] 1.44368 0.55568 -0.630277
> [386,] -0.19104 0.61441 0.514243
> [387,] -0.66882 -0.06045 1.426089
> [388,] 1.86402 -0.68995 0.228943
> [389,] 0.06095 -1.82778 0.302257
> [390,] 0.13685 -0.72720 0.019238
> [391,] 0.97705 0.79508 0.181438
> [392,] -0.92785 -0.84554 -0.760591
> [393,] 0.04939 -0.55932 0.260846
> [394,] 1.30886 -0.67049 0.406676
> [395,] -0.20378 -0.81770 0.874419
> [396,] -0.91348 0.62812 1.377931
> [397,] -0.01459 -0.36610 0.976352
> [398,] -0.69443 0.20886 -0.211351
> [399,] 0.18576 -0.06839 -0.822864
> [400,] -0.49669 -0.34962 -0.296680
> [401,] 1.27666 0.38571 1.034192
> [402,] -1.14927 0.21575 -0.478247
> [403,] -0.11588 0.36580 -0.267516
> [404,] 1.13835 -0.33799 0.745534
> [405,] -0.45256 -1.48788 0.393459
> [406,] -0.27956 -0.10200 -0.140999
> [407,] -1.00412 -0.05541 1.438384
> [408,] 0.81347 -1.25384 0.698627
> [409,] 0.45480 -0.60781 0.387385
> [410,] 0.86309 0.06221 0.528187
> [411,] -0.18675 -0.72675 1.302956
> [412,] -0.64424 -1.16993 0.270698
> [413,] 0.95631 -0.03485 0.323155
> [414,] -0.41651 0.51591 0.798723
> [415,] 0.00055 0.96957 -0.645252
> [416,] 0.33199 -0.60437 0.104745
> [417,] -0.82448 0.48150 0.211128
> [418,] 1.43005 -0.20914 0.119165
> [419,] -0.16739 0.33395 0.229167
> [420,] 0.58930 -0.37437 0.065063
> [421,] 0.20977 -0.54628 -0.536032
> [422,] -1.11997 -0.58429 0.462717
> [423,] -0.40402 0.92504 -0.515688
> [424,] 1.83903 -0.10038 0.836719
> [425,] -0.28930 -1.09939 0.484685
> [426,] 0.21270 0.27533 -0.609612
> [427,] 0.51170 -0.41357 0.404414
> [428,] 0.53900 -0.54828 0.882568
> [429,] -1.39727 0.34059 -0.580829
> [430,] -0.01380 0.52519 -0.520526
> [431,] -0.59480 -0.95094 0.614800
> [432,] 1.58322 0.43127 0.469598
> [433,] 0.12147 0.65743 0.784547
> [434,] -0.33561 0.22418 -0.188947
> [435,] -0.40494 -0.27930 -0.166831
> [436,] -1.78965 0.15412 0.082562
> [437,] -0.21693 0.18305 0.101418
> [438,] 0.47379 -0.06431 0.464622
> [439,] 0.86646 0.09650 -0.724021
> [440,] -0.45103 -0.11099 -0.307164
> [441,] -1.11906 0.55226 0.284891
> [442,] -0.84318 0.20339 0.406598
> [443,] -0.70096 0.01799 0.163462
> [444,] 1.04615 0.21521 0.312986
> [445,] -0.36443 0.07644 -0.511958
> [446,] 0.30815 -0.34895 -0.135539
> [447,] -0.77007 -0.82796 -0.539336
> [448,] -0.98932 0.05354 -0.312516
> [449,] -0.44476 0.43003 -0.548188
> [450,] -0.88631 -0.29373 -0.952403
> [451,] -0.51062 -0.94689 -1.046924
> [452,] -0.43334 -0.41703 -1.777777
> [453,] -1.18608 0.80956 0.737901
> [454,] 0.26510 -0.20805 0.540262
> [455,] -1.22825 0.20640 0.281669
> [456,] -0.11349 -0.33348 0.222914
> [457,] -0.65008 -0.46775 -0.086582
> [458,] 0.22179 0.01446 0.407965
> [459,] 1.11054 -0.82442 -0.456806
> [460,] 0.89626 -1.04482 -0.556402
> [461,] 0.38603 -0.55465 0.846175
> [462,] 0.70497 0.17616 -0.729173
> [463,] -1.60433 -0.15992 0.519124
> [464,] 0.65776 -0.48668 -0.536218
> [465,] -0.72347 -0.79815 -0.097501
> [466,] -1.58807 -0.38819 1.505076
> [467,] -0.35676 0.60796 -0.544321
> [468,] -0.32351 -0.04916 0.181867
> [469,] -0.74455 -0.43092 0.412614
> [470,] 0.01446 0.43787 0.858690
> [471,] 1.09513 -0.92987 0.489264
> [472,] -1.24138 -0.15590 -0.310609
> [473,] -1.75062 0.27055 -0.031332
> [474,] -0.70079 1.38709 -1.128690
> [475,] -0.46024 -0.03715 -0.127745
> [476,] -0.47944 -0.68284 0.290525
> [477,] 0.95117 -0.16706 0.261961
> [478,] 1.49086 -0.06219 0.087199
> [479,] 0.09001 -0.27006 0.199347
> [480,] -1.27074 0.08907 0.360950
> [481,] 0.05031 0.37567 -0.354565
> [482,] 0.43263 -0.07188 -0.376423
> [483,] 0.41661 1.27180 0.495694
> [484,] 1.21374 0.79112 0.395911
> [485,] 1.23881 1.31816 0.579235
> [486,] 0.93056 0.10853 -1.101901
> [487,] -0.88367 0.42990 0.363537
> [488,] 0.15798 0.84335 0.806532
> [489,] -1.97494 0.43747 1.004816
> [490,] 0.25948 0.03084 -0.605225
> [491,] -1.46092 0.09689 0.748804
> [492,] 1.63121 0.29443 0.041260
> [493,] 0.77078 0.74413 -0.485693
> [494,] 1.47771 0.44470 -0.366460
> [495,] -0.52713 0.26032 0.195517
> [496,] -1.77483 -1.32954 0.431818
> [497,] 2.15328 -0.90404 0.399704
> [498,] -0.09215 -0.35912 -0.612312
> [499,] 0.58459 0.42226 -0.419838
> [500,] 1.83417 -0.44346 0.293011
> [501,] 0.16381 -0.83302 -1.425063
> [502,] 0.34142 -0.08463 -0.537581
> [503,] -1.39970 -1.29848 0.457295
> [504,] 1.12291 0.03779 -0.130319
> [505,] 0.07089 0.63510 -0.720080
> [506,] 0.27509 -0.60385 -0.265576
> [507,] -1.64634 -0.50337 -0.518572
> [508,] -1.72592 0.42380 -0.223833
> [509,] -0.37786 0.09651 0.122380
> [510,] -0.79010 -1.47491 0.154296
> [511,] 0.02388 -0.07540 -0.736831
> [512,] -0.43903 0.36763 -0.069755
> [513,] 0.50565 0.87603 -0.126821
> [514,] -0.03577 -0.57078 -0.089929
> [515,] -0.16896 -0.46195 0.087702
> [516,] -0.39903 0.10346 -0.680496
> [517,] -0.35431 0.45841 -0.662897
> [518,] 1.76033 0.43322 0.652647
> [519,] 0.98478 -0.54026 -1.914602
> [520,] 1.45753 -0.98461 0.205854
> [521,] 1.77306 -0.59561 -0.357027
> [522,] 0.09873 -1.23250 -0.755270
> [523,] -0.50245 -0.86165 0.579785
> [524,] 0.92275 0.48659 -0.035206
> [525,] -0.41360 -0.90545 0.454309
> [526,] 0.32531 0.34370 -0.736348
> [527,] 1.14229 0.00949 0.184786
> [528,] -0.32221 -0.57189 -0.126943
> [529,] -0.11059 -1.03184 0.878596
> [530,] 0.97721 0.14640 -1.099916
> [531,] 0.55929 0.26347 0.723967
> [532,] 1.74585 1.11444 0.002733
> [533,] -1.51729 -0.48058 -0.309608
> [534,] -0.76027 0.95219 -0.242572
> [535,] 0.79158 0.16687 1.033396
> [536,] -0.18159 -0.39598 1.176274
> [537,] -1.20870 0.25652 0.074042
> [538,] -1.18920 0.21829 0.105148
> [539,] 0.23239 0.19713 -0.259996
> [540,] 0.87332 0.20464 0.331284
> [541,] -0.24447 0.18395 0.307492
> [542,] 1.03938 -1.55661 -0.456260
> [543,] 0.41200 -0.18069 -0.059858
> [544,] 0.31538 0.88190 1.076151
> [545,] -0.02860 0.62930 1.209828
> [546,] 1.75216 0.03884 0.366975
> [547,] 0.14519 0.65410 0.319849
> [548,] 0.56229 0.60793 -0.438190
> [549,] -1.13205 0.46319 1.067935
> [550,] -0.40453 -0.42594 0.078046
> [551,] -0.60662 -1.07105 -0.027671
> [552,] 0.93800 -0.62258 -0.534508
> [553,] -0.28281 0.20082 -0.217598
> [554,] -0.63646 0.10114 -0.841679
> [555,] -0.39908 -0.60743 -0.129885
> [556,] -1.72069 -1.12001 0.018838
> [557,] -0.35823 0.59221 -0.366177
> [558,] -0.98268 0.01113 -0.725684
> [559,] 0.26837 -0.00383 0.469915
> [560,] 1.08203 0.52091 -0.146671
> [561,] -0.70238 -0.34666 -0.456091
> [562,] 0.43520 -0.27843 -0.502703
> [563,] -0.13641 1.14710 -0.712778
> [564,] -1.30729 0.92807 0.473049
> [565,] -1.82119 1.26209 -0.992294
> [566,] -0.65999 1.60465 0.394147
> [567,] -1.09816 0.79374 0.082250
> [568,] -1.53987 -0.01694 -1.320863
> [569,] -0.88871 -1.35122 -0.431765
> [570,] -0.28757 -0.16263 0.413989
> [571,] 0.12577 -1.24723 0.145452
> [572,] 0.21388 0.88245 -0.050297
> [573,] 1.25079 0.12336 -0.467852
> [574,] -0.74117 0.49006 0.355960
> [575,] -0.35830 -0.19524 0.207228
> [576,] 0.38857 -0.78682 -0.017537
> [577,] -0.92018 0.06124 0.283730
> [578,] -1.08115 -0.66693 -0.070281
> [579,] 0.67258 -0.38055 0.196324
> [580,] 0.22928 1.08180 -0.886702
> [581,] -0.27395 1.02415 -0.517330
> [582,] -0.63148 0.43128 -0.385444
> [583,] 1.69891 0.97551 0.115331
> [584,] 1.42372 0.04413 0.501831
# Extraire les loadings
loadings(res.fa)
>
> Loadings:
> Factor1 Factor2 Factor3
> i1 0.474
> i2 0.375
> i3 0.430
> i4 0.711 0.153
> i5 0.716 -0.173
> i6 0.691 0.229
> i7 0.247
> i8 0.403
> i9 0.326
>
> Factor1 Factor2 Factor3
> SS loadings 1.498 0.586 0.421
> Proportion Var 0.166 0.065 0.047
> Cumulative Var 0.166 0.232 0.278
# ou pour voir tous les loadings
head(res.fa$loadings[])
> Factor1 Factor2 Factor3
> i1 0.0238 0.4743 0.06556
> i2 0.0285 0.3752 -0.04153
> i3 0.0194 0.4300 0.05369
> i4 0.7109 0.1527 0.00653
> i5 0.7163 0.0547 -0.17282
> i6 0.6906 -0.0862 0.22903