3 Calculer

Dans cette section, les fonctions essentielles couramment utilisées sont présentées en rafale. L’accent est mis sur la définition de la fonction (qu’est-ce qu’elle fait?) et son utilité (à quoi sert-elle?). Pour les fonctions essentielles de nature statistiques (moyennes, médianes, etc.), cette section développe une fonction maison (rédigée par l’utilisateur pour la mettre en pratique) et identifie la fonction déjà implantée en R.

3.1 La longueur

La longueur d’une variable correspond au nombre d’éléments qu’elle contient. La fonction length() permettra d’obtenir ce résultat. Ce sera particulièrement utile lorsqu’il faudra calculer, par exemple, le nombre de boucle à réaliser à partir des éléments d’un vecteur ou la taille d’échantillon (le nombre d’unités d’observation d’une variable).

La somme d’une chaîne de caractères est toujours de \(1\), peu importe le nombre de caractères. La fonction nchar() produira le nombre de caractères.

Une variable qui existe, mais qui ne contient pas de valeur aura une longueur égale à \(0\). Ce type de variable est utile lorsqu’il faut créer une variable dont la taille sera altérée.

x <- c(1, 2, 3)
length(x)
> [1] 3

y <- "Bonjour tout le monde!"
length(y)
> [1] 1

nchar(y)
> [1] 22

Pour les matrices et les jeux de données, ncol() (nombre de colonnes) et nrow() (nombre de lignes) sont plus efficaces et intuitives.

3.2 La répétion

La fonction rep() est utile pour répéter volontairement des valeurs. Il y trois possibilités de répétitions: l’argument times définit le nombre de fois que le vecteur est répété; l’argument each définit le nombre de fois que chaque élément est répété; l’argument length.out précise le nombre d’éléments de la sortie. Plusieurs combinaisons de ces arguments sont possibles.

vec <- c(2, 4, "chat")

# Répéter `vec` trois fois
rep(vec, times = 3)
> [1] "2"    "4"    "chat" "2"    "4"    "chat" "2"    "4"   
> [9] "chat"

# Répéter chaque élément de `vec` trois fois
rep(vec, each = 3)
> [1] "2"    "2"    "2"    "4"    "4"    "4"    "chat" "chat"
> [9] "chat"

# Répéter chaque élément de `vec` d'une longueur de 8
rep(vec, length.out = 8)
> [1] "2"    "4"    "chat" "2"    "4"    "chat" "2"    "4"

#  Répéter chaque élément 3 fois à 2 reprises
rep(vec, times = 2, each = 3)
>  [1] "2"    "2"    "2"    "4"    "4"    "4"    "chat" "chat"
>  [9] "chat" "2"    "2"    "2"    "4"    "4"    "4"    "chat"
> [17] "chat" "chat"

3.3 La séquence

Une première fonction pour créer des séquences de nombres est l’utilisation de : avec un nombre avant et après la ponctuation.

# 1:3 équivaut à c(1, 2, 3)
1:3
> [1] 1 2 3

Pour plus de malléabilité, la fonction seq() génère une séquence régulière de valeurs. Les arguments sont seq(from = , to = , by = ) traduisibles par de , à, par. Les arguments par défaut seront très utiles pour simplifier l’écriture; La fonction commence ou termine la séquence par 1 et fera des bonds de 1 entre les valeurs. Un autre argument est la longueur de la sortie length.out qui spécifie le nombre d’éléments que devra comporter le vecteur de sortie.

# Une séquence de 1 (défaut, from = 1) à 10
seq(10)
>  [1]  1  2  3  4  5  6  7  8  9 10

# Une séquence de 1 (défaut, from = 1) à -10
seq(-10)
>  [1]   1   0  -1  -2  -3  -4  -5  -6  -7  -8  -9 -10

# Une séquence de -10 (défaut, from = 1) à 1
seq(from = -10, to = 1)
>  [1] -10  -9  -8  -7  -6  -5  -4  -3  -2  -1   0   1

# Une séquence de nombres paires (from = 2, to = 10, by = 2)
seq(2, 10, 2)
> [1]  2  4  6  8 10

# Une séquence de nombres paires 
seq(from = 2, by = 2, length.out = 5)
> [1]  2  4  6  8 10

3.4 La somme

Il est possible de calculer des sommes de variables pour en obtenir le total. En tant qu’humain, le calcul d’une série de nombre correspond à prendre chaque nombre et de les additionner un à un. La fonction suivante reproduit assez bien ce qu’un humain ferait (avec ses quelques caprices de programmation tel que devoir déclarer l’existence de la variable de total et spécifier le nombre d’éléments à calculer).

somme <- function(x){
  # La taille du vecteur `x`
  n <- length(x)
  
  # Définir une variable nulle
  total <- 0
  
  # Boucle pour additionner chaque élément
  for(i in 1:n){
    
    # Prendre le ie élément et l'additionner
    # au total des (i-1)e éléments précédents
    total <- total + x[i]
  }
  # Retourner le total après la boucle
  return(total)
}

# Pour tester
x <- c(1,2,3,4,5,-6)
somme(x)
> [1] 9
sum(x)
> [1] 9

À noter que l’utilisation de la boucle est à des fins illustratives seulement. En termes de rendement computationnel, elle est bien peu efficace. Il faudra privilégier la fonction sum() pour calculer le total de son entrée.

Il faut prendre garde : R calcule le total de tous les éléments de l’entrée sans égard aux lignes et aux colonnes. Autrement dit, il vectorise les entrées. Si deux variables étaient entrées par inadvertance, alors R calculerait la somme de ces deux variables plutôt que de retourner deux totaux. À cette fin, les fonctions rowSums() et colSums() seront utiles lorsqu’il faudra calculer des sommes sur des lignes (row) ou des colonnes (col).

3.5 La moyenne

La moyenne est une mesure de tendance centrale qui représente le centre d’équilibre d’une distribution (un centre de gravité en quelque sorte). Si le poids d’un des côtés d’une distribution de probabilité était altéré (plus lourde ou plus légère), alors la moyenne se déplacerait relativement vers cette masse.

La moyenne d’un échantillon correspond à la somme de toutes les unités d’une variable divisée par le nombre de données de cette variable ou, mathématiquement, \[\bar{x}=\frac{\Sigma_{i=1}^n x}{n}\] où \(x\) est la variable, \(n\) est le nombre d’unité et \(\Sigma_i^n\) représente la somme de toutes les unités de \(x\). R possède déjà une fonction permettant de calculer la moyenne sans effort, mean() où l’argument est la variable. Il est possible de développer une fonction maison pour calculer la moyenne comme

x_bar <- sum(x)/length(x)

où sum(x) calculer la somme de toutes les unités de x, / permet la division et length(x) calcule le nombre d’unités du vecteur x. Par exemple, à partir d’une variable x, les fonctions suivantes donnent le même résultat. Par contre la fonction mean() est beaucoup plus robuste que cette dernière équation.

# Un vecteur
x <- c(0, 1, 2, 3, 4, 5)

# Comparaison
mean(x)
> [1] 2.5
sum(x)/length(x)
> [1] 2.5

Comme pour sum(), les fonctions rowMeans() et colMeans() seront utiles lorsqu’il faudra calculer des moyennes sur des lignes (row) ou des colonnes (col).³

3.6 La médiane

La médiane d’un échantillon correspond à la valeur où \(50\%\) des données se situe au-dessous et au-dessus de cette valeur. C’est la valeur au centre des autres (lorsqu’elles sont ordonnées). Quand le nombre de données est impair, le \(\frac{(n+1)}{2}\)^e élément est la médiane. Quand le nombre est pair, la moyenne des deux valeurs au centre correspond à la médiane. Cette statistique est intéressante comme mesure de tendance centrale, car elle est plus robuste aux valeurs aberrantes (moins sensibles) que la moyenne.

Évidemment, R offre déjà une fonction median() pour réaliser le calcul. Il est toutefois possible de programmer une fonction maison. Il faut utiliser la fonction sort() pour ordonner les données (croissant par défaut).

mediane <- function(x) {
  # Longueur du vecteur
  n <- length(x)
  
  # Ordonner le vecteur
  s <- sort(x)
  # Vérifier si la longueur est paire ou impaire et
  # alors calculer la valeur médiane correspondante
  ifelse(n%%2 == 1, s[(n + 1) / 2], mean(s[n / 2 + 0:1]))
}

# Un vecteur
x <- c(42, 23, 53, 77, 93, 20, 37, 24, 60, 62)

# Comparaison
median(x)
> [1] 47.5
mediane(x)
> [1] 47.5

L’expression n%%2, lue \(n \bmod 2\), joue astucieusement le rôle de vérifier si n est impaire. La formule générale \(x \bmod y\) représente une opération binaire associant à deux entiers naturels le reste de la division du premier par le second. Par exemple, \(60 \bmod 7\), noter 60%%7 dans R, donne \(4\) soit le reste de \(7*8 + 4 = 60\). Le logiciel le confirme.

60%%7
> [1] 4

Il s’agit d’une technique de programmation très pratique. Dans le cas de n%%2, la formule donne \(1\) dans le cas d’un nombre impair ou \(0\) dans le cas d’un nombre pair, puis teste ce résultat pour déterminer s’il réalise s[(n+1)/2] lorsque n%%2==1(TRUE) , ce qui correspond à choisir l’élément au centre d’un vecteur de taille impair, ou bien mean(s[n/2+0:1] lorsque n%%2==0(FALSE) , ce qui correspond à choisir les deux éléments au centre d’un vecteur pair et d’en faire la moyenne. Il s’agit de l’une des nombreuses façons selon lesquelles il est possible de programmer la médiane.

3.7 La variance

La variance d’un échantillon est une mesure de dispersion. Elle représente la somme des écarts (distances) par rapport à la moyenne au carré divisée par la taille d’échantillon moins \(1\). Mathématiquement, il s’agit de l’équation (3.1).

\[ s^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2 \tag{3.1} \] Il est assez aisé d’élaborer une fonction pour réaliser se calculer avec les fonctions déjà abordées.

variance <- function(x){
  # Longueur du vecteur
  n <- length(x)
  
  # Moyenne du vecteur
  xbar <- mean(x)
  
  # La variance
  variance <- sum((x - xbar) ^ 2)/(n - 1)
  return(variance)
}

La variance peut aussi être calculée plus efficacement avec la fonction R var().

# Un vecteur
x <- c(26, 6, 40, 36, 14, 3, 21, 48, 43, 2)

# Comparaison
variance(x)
> [1] 300
var(x)
> [1] 300

3.8 L’écart type

L’écart type d’un échantillon représente la racine carrée de la variance. Elle a une interprétation plus intuitive en tant que mesure de la moyenne des écarts par rapport à la moyenne. Si le calcul avait été entrepris avec les distances par rapport à la moyenne (au lieu des écarts au carré), alors la somme serait toujours de 0, un résultat tout à fait bancal. En prenant la racine carrée des écarts au carré, ce qui constitue une mesure de distance euclidienne, l’écart type devient une mesure de l’étalement de la dispersion autour du centre d’équilibre.

\[ s =\sqrt{s^2}= \sqrt{\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2} \] Avec R, la fonction de base est sd(). Il est possible de récupérer la fonction maison précédemment rédigée.

ecart.type <- function(x){
  # La racine carrée de la variance
  et <- sqrt(variance(x))
  return(et)
}

# Comparaison
ecart.type(x)
> [1] 17.3
sd(x)
> [1] 17.3

3.9 L’asymétrie

L’asymétrie (skewness) est une mesure couramment utilisée de symétrie d’une distribution. Une distribution symétrique, comme la distribution normale, implique que la densité des observations est approximativement égale des deux côtés de la moyenne (valeurs plus hautes et plus basses). Une asymétrie négative indique que la distribution est asymétrique à gauche et que la moyenne des données (moyenne) est inférieure à la valeur médiane. Une asymétrie positive indique l’inverse, c’est-à-dire qu’une distribution est asymétrique à droite. Une distribution asymétrique droite est biaisée vers les valeurs les plus élevées, de sorte que la moyenne de la distribution est supérieure à la médiane de la distribution.

Le calcul d’asymétrie correspond au ratio entre le troisième moment (écarts au cube) de la distribution par rapport à la racine carré du deuxième moment au cube. Plus simplement, le calcul peut aussi se voir comme le ratio entre la moyenne des écarts centrés au cube par rapport à l’écart type au cube.

\[ \gamma_1 = \frac{\sum_{i=1}^n(x_i-\bar{x})^3}{\Big(\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2}\Big)^3} \]

Et en code R.

asymetrie <- function(x){
  n <- length(x)           # Nombre de données
  x <- x - mean(x)         # Centrer les données
  skew <- sum(x^3) /       # Écarts au cube divisés par
          sqrt(sum(x^2))^3 # l'écart type au cube
  return(skew)
}

R de base ne contient pas de fonction permettant de calculer l’asymétrie. Il faut utiliser le package moments pour obtenir la fonction requise, moments::skewness() ou psych avec psych::skew(). Plusieurs autres packages offrent des fonctions.

moments::skewness(x)
psych::skew(x)

3.10 L’aplatissement

L’aplatissement (kurtosis) est une mesure de la propension d’une distribution à produire des valeurs éloignées de la moyenne. Souvent erronément référée comme une mesure de la pointe (peakedness; planéité, pointu ou modalité), l’aplatissement réfère à l’épaisseur des queues de la distribution (Westfall, 2014). Plus elles sont épaisses, et plus les valeurs ont tendances à être éloignées (les valeurs extrêmes sont fréquentes). Plus elles sont minces, plus les valeurs ont tendances à être près de la moyenne (les valeurs extrêmes sont rares).

Comme l’asymétrie, le calcul se base sur le ratio du quatrième moment (écarts bicarrés⁴) sur la racine du deuxième moment des écarts bicarrés. Plus simplement, il s’agit du ratio de la moyenne des écarts centrés de degré 4 divisée par la racine carré des écarts

\[ \beta_2 = \frac{\sum_{i=1}^n(x_i-\bar{x})^4}{\Big(\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2}\Big)^4} \]

Comme la valeur de l’aplatissement tend vers 3, les statisticiens soustraient cette valeur à l’aplatissement \(\beta_2\) pour la centrer sur \(0\).

\[ \gamma_2 = \beta_2-3 \] L’aplatissement \(\beta_2\) représente l’aplatissement régulier et l’aplatissement \(\gamma_2\) correspond à l’aplatissement excessif.

En code R.

aplatissement <- function(x){
  n <- length(x)            # Nombre de données
  x <- x - mean(x)          # Centrer les données
  kurt <- mean(x^4) /       # Écarts bicarrés divisés par
          sqrt(mean(x^2))^4 # l'écart type au bicarré
  return(kurt)
}

R de base ne contient pas de fonction permettant de calculer l’aplatissement. Il faut utiliser le package moments pour obtenir la fonction requise moments::kurtosis() ou psych avec psych::kurtosi(). Il faut noter que moments calcule l’aplatissement régulier et que, dans le cas de psych, il y a plusieurs types d’aplatissement, le plus commun étant le type 1 (aplatissement excessif). Le type 3 est toutefois plus désirables comme il n’est pas biaisé. Plusieurs autres packages offrent des fonctions pour calculer l’aplatissement.

moments::kurtosis(x) - 3
psych::kurtosi(x, type = 1)

3.11 Les graines

Par souci de reproductibilité, il est possible de déclarer une valeur de départ aux variables pseudoaléatoires, ce que l’on nomme une graine ou seed en anglais. Cela permet de toujours d’obtenir les mêmes valeurs à plusieurs reprises, ce qui est très utile lors d’élaboration de simulations complexes ou lorsque des étudiants essaient de répliquer les résultats tirés d’un ouvrage pédagogique.

set.seed("nombre")

Il suffit de spécifier cette commande (en remplaçant nombre par un nombre) en début de syntaxe pour définir la séquence de nombre. Cette fonction sera utilisée à plusieurs reprises dans le but de reproduire les mêmes sorties.

Cette fonction est présentée, car elle reviendra régulièrement dans ce livre pour qu’il soit possible de reproduire et obtenir exactement les mêmes résultats.

3.12 Les distributions

Il existe plusieurs distributions statistiques déjà programmées avec R. Voici les principales utilisées dans cet ouvrage.

Table 3.1: Noms des distributions, fonctions et leurs arguments

Distribution	R	Arguments
binomiale	binom	size, prob
Khi-carré	chisq	df, ncp
Fisher	f	df1, df2, ncp
normale	norm	mean, sd
student	t	df, ncp
uniform	unif	min, max

Les libellés ci-dessus ne commanderont pas de fonction. Il faut joindre en préfixe à ces distributions l’une des quatre lettres suivantes : d, p,q, ou r. La plus simple est certainement r (random) qui génère n valeurs aléatoires de la distribution demandée selon les paramètres spécifiés. Les fonctions q (quantile) prennent un argument de 0 à 1 (100%), soit un percentile et retourne la valeur de la distribution. La fonction p (probabilité) retourne la probabilité cumulative (du minimum jusqu’à la valeur) d’une valeur de cette distribution. Enfin, la lettre d (densité) permet, notamment, d’obtenir les valeurs de densité de la distribution.

Voici un exemple avec la distribution normale.

set.seed(9876)

# Génère 5 valeurs aléatoires en fonction des paramètres
rnorm(n = 5, mean = 10, sd = .5)
> [1] 10.51  9.42  9.90  9.95 10.01

# Retourne les valeurs associés à ces probabilités
qnorm(p = c(.025,.975))
> [1] -1.96  1.96

# Retourne la probabilité d'obtenir un score de 1.645 et moins
pnorm(q = c(.5, 1.645, 1.96))
> [1] 0.691 0.950 0.975

# La valeur de la densité de la distribution
dnorm(x = c(0, 1))
> [1] 0.399 0.242

Ces quatre lettres peuvent être associées à toutes les distributions énumérées et bien d’autres. Elles respectent toutes ce cadre.

Afin d’illustrer ce que font ces variables, la Figure 3.1 montre dnorm(), pnorm() et qnorm(). La fonction rnorm() n’est pas illustrée. Cette dernière retourne des valeurs de l’axe des \(x\) en respectant les probabilités d’une courbe normale. La fonction dnorm() prend en argument une valeur de l’axe des \(x\) et retourne la valeur de la courbe normale (la densité) correspondante, soit la courbe illustrée. En d’autres termes, elle retourne la hauteur de la courbe (ligne pointillée). Les fonctions pnorm() et qnorm() sont interreliées. La fonction pnorm() prend une valeur de l’axe des \(x\) et retourne sa probabilité (de \(-\infty\) à \(x\)), soit la zone grise de la Figure 3.1. La fonction qnorm(), quant à elle, prend une probabilité et retourne la valeur sur l’axe des \(x\) correspondant.

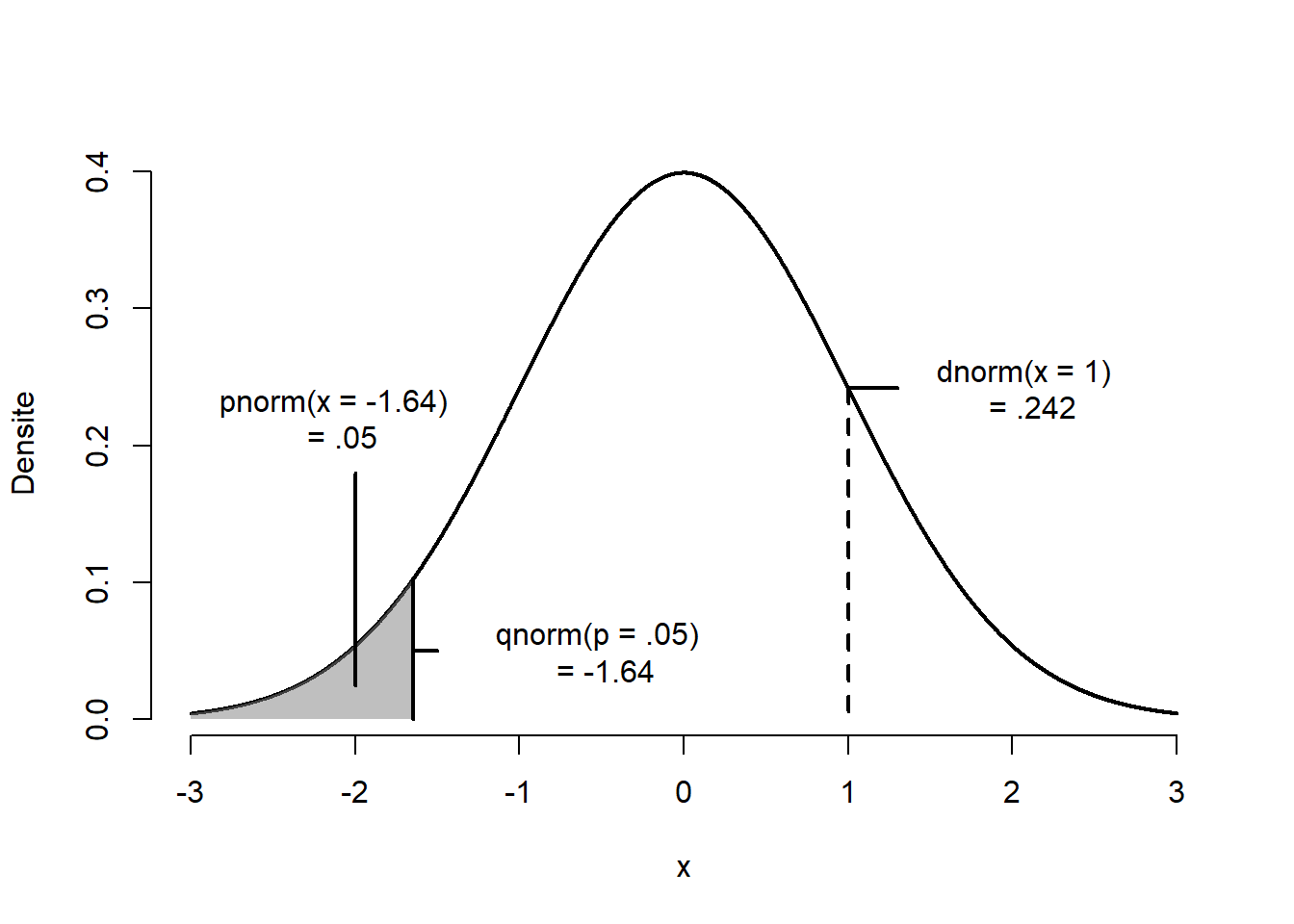
Figure 3.1: Illustration des fonctions liées à la distribution normale

Ces fonctions entreront en jeu dans le chapitre Inférer.