11 Analyser

En continuation de l’introduction des théories des tests d’hypothèses (voir Inférer) et l’aperçu donnée par le test-\(t\) à échantillon unique, cette section poursuit la présentation en introduisant des analyses statistiques de bases comme les différences de moyennes, l’association linéaire et les tests pour données nominales. Les tests-\(t\) indépendant et dépendant, la covariance, la corrélation ainsi que le test du \(\chi2\) pour table de contingence sont présentées.

11.1 Les différences de moyennes

11.1.1 Le test-\(t\) indépendant

En général, l’expérimentateur ne s’intéresse pas à comparer une moyenne à une valeur arbitraire, comme c’était le cas avec le test-\(t\) à échantillon unique. Cela peut lui être assez trivial. Il s’intéresse plutôt à comparer une moyenne à une autre moyenne, soit une différence entre deux groupes indépendants, par exemple, quelle est la différence entre un groupe traitement et un groupe contrôle?

En se basant sur le test \(t\) à échantillon unique, la valeur-\(t\) pour deux moyennes se calcule selon l’équation (11.1)

\[\begin{equation} t_{n-2} = \frac{\bar{x_1}-\bar{x_2}}{\sqrt{\frac{s^2_{1}}{n_1}+\frac{s^2_{2}}{n_2}}} \tag{11.1} \end{equation}\]

où l’indice de la valeur-\(t\) est le nombre de degrés de liberté \(n-2\). Comme deux variances sont estimées, deux degrés de libertés sont imputés, ce qui octroi \(n-2\) degrés. En plus de considérer \(\bar{x_2}\) la valeur arbitaire de comparaison (l’ordre de \(\bar{x_2}\) et \(\bar{x^1}\) est arbitraire), les deux écarts types sont également considérés au dénominateur.

Une fois le calcul réalisé, la logique du test d’hypothèse est la même, à l’exception de l’hypothèse nulle qui correspond maintenant à l’absence de différence entre les deux moyennes.

Voici un exemple de programmation du test-\(t\) pour deux groupes indépendants.

testt.ind <- function(x1, x2){
  # x1 est une variable continue associée au groupe 1
  # x2 est une variable continue associée au groupe 2
  
  # Calcul des moyennes
  x1bar <- mean(x1) ; x2bar <- mean(x2)
  
  # Calcul des variances
  x1var <- var(x1) ; x2var <- var(x2)
  
  # Calcul des tailles d'échantillon
  nx1 <- length(x1) ; nx2 <- length(x2)
  
  # Valeur-t, degrés de liberté et valeur-p
  vt <- (x1bar - x2bar) / sqrt(x1var / nx1 + x2var / nx2)
  dl <- nx1 + nx2 - 2
  vp <- (1 - pt(abs(vt), df = dl)) * 2 
  statistique <- list(valeur.t = vt, dl = dl, valeur.p = vp)
  return(statistique)
}

Pour générer un exemple de données, le code ci-après crée un échantillon de 15 unités réparties en deux groupes, le premier groupe (gr0) est tiré d’une distribution normale ayant une moyenne de 1 et un écart type de 1, le deuxième groupe (gr1), une moyenne de 0 et un écart type de 1. La syntaxe illustre la création de deux variables pour créer les deux groupes. Il est aussi possible d’envisager la création sur en termes d’équation linéaire, comme l’équation (11.2),

\[\begin{equation} y = \mu_0 + \mu_1x_1 + \epsilon \tag{11.2} \end{equation}\]

où \(y\) est le score observé des unités et les autres variables construisent ce score, \(\mu_0\) correspond à la moyenne du groupe référent de population (le groupe contrôle en quelque sorte.), \(\mu_1\) réfère à la différence de moyenne entre les deux groupes identifiés par \(x_1\) qui réfère à l’assignation au groupe, soit 0 pour le groupe contrôle et 1 pour le groupe différent. Pour ce même exemple, \(\mu_1 = -1\). Par le produit \(\mu_1x_1\), le groupe contrôle associé à la valeur 0 n’a pas de modification de la moyenne, \(-1*0=0\) alors le groupe différent associé à la valeur 1, \(-1*1=-1\). Enfin, \(\epsilon\) correspond à la variabilité entre les unités. Cette façon de programmer la création des variables illustre bien l’association linéaire qui existe même dans les différences de moyennes et sera très utile pour des modèles plus compliqués.

# Un exemple de jeu de données programmé de deux façons
# Méthode 1
set.seed(2021)
gr0 <- rnorm(n = 15, mean = 1, sd = 1)
gr1 <- rnorm(n = 15, mean = 0, sd = 1)

# Méthode 2
set.seed(2021)

x1 <- c(rep(0, 15), rep(1, 15)) # Appartenance au groupe (0 et 1)
e  <- rnorm(n = 30, mean = 0, sd = 1) # Erreur interindividuel
mu0 <- 1  # La moyenne du groupe référent
mu1 <- -1 # Le deuxième groupe a une différence de moyenne de -1

y <- mu0 + mu1 * x1 + e

# Présenter quelques participants; retirer les crochets pour voir tous
(cbind(method1 = c(gr0, gr1), method2 = y))[10:20,]
>       method1 method2
>  [1,]  2.7300  2.7300
>  [2,] -0.0822 -0.0822
>  [3,]  0.7272  0.7272
>  [4,]  1.1820  1.1820
>  [5,]  2.5085  2.5085
>  [6,]  2.6045  2.6045
>  [7,] -1.8415 -1.8415
>  [8,]  1.6233  1.6233
>  [9,]  0.1314  0.1314
> [10,]  1.4811  1.4811
> [11,]  1.5133  1.5133

Les données sont identiques.

Une fois la fonction créée, il est possible de la tester et de la comparer avec la fonction R de base test.t().

# Vérification de la fonction maison
testt.ind(gr0, gr1)
> $valeur.t
> [1] 3.4
> 
> $dl
> [1] 28
> 
> $valeur.p
> [1] 0.00205

# Comparer avec la fonction R
t.test(gr0, gr1, var.equal = TRUE)
> 
>   Two Sample t-test
> 
> data:  gr0 and gr1
> t = 3, df = 28, p-value = 0.002
> alternative hypothesis: true difference in means is not equal to 0
> 95 percent confidence interval:
>  0.54 2.18
> sample estimates:
> mean of x mean of y 
>     1.332    -0.029

Les équations et codes précédents ne sont adéquats que si les variances sont égales entre les deux groupes. Cette notion est quelque peu trahie par la spécification dans la fonction R de l’argument var.equal = TRUE qui par défaut est FALSE. Pour un test-\(t\) indépendant suivant les règles de l’art, il faut appliquer une correction (approximation de Welsh) aux degrés de liberté. Les degrés de liberté deviennent moins élégants et respectent l’équation (11.3).

\[\begin{equation} dl=\frac{\left(\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}\right)^2}{\frac{\left(\frac{s^2_1}{n_1}\right)^2}{n_1-1}+\frac{\left(\frac{s^2_2}{n_2}\right)^2}{n_2-1}} \tag{11.3} \end{equation}\]

En apportant cette correction au code initial.

testt.ind2 <-function(x1, x2){
  # x1 est une variable continue associée au groupe 1
  # x2 est une variable continue associée au groupe 2
  x1bar <- mean(x1) ; x2bar <- mean(x2)  # Les moyennes
  x1var <- var(x1) ; x2var <- var(x2)    # Les variances
  nx1 <- length(x1) ; nx2 <- length(x2)  # Les tailles
  
  # L'erreur type 
  et <- sqrt(x1var / nx1 + x2var / nx2)
  
  # Valeur-t
  vt <- (x1bar - x2bar) / et
  
  # Correction des degrés de liberté
  dl <- et^4 / 
    ((x1var^2 / (nx1^2 * (nx1 - 1))) + 
       (x2var^2 / (nx2^2 * (nx2 - 1))))
  
  # Valeur-p
  vp <- (1 - pt(abs(vt), df = dl)) * 2 
  
  statistique <- list(valeur.t = vt, dl = dl, valeur.p = vp)
  return(statistique)
}

Le voici comparé à la fonction R de base.

t.test(gr0, gr1) # Absence de l'argument var.equal = TRUE
> 
>   Welch Two Sample t-test
> 
> data:  gr0 and gr1
> t = 3, df = 27, p-value = 0.002
> alternative hypothesis: true difference in means is not equal to 0
> 95 percent confidence interval:
>  0.539 2.182
> sample estimates:
> mean of x mean of y 
>     1.332    -0.029
testt.ind2(gr0, gr1)
> $valeur.t
> [1] 3.4
> 
> $dl
> [1] 26.9
> 
> $valeur.p
> [1] 0.00213

Les sorties sont identiques.

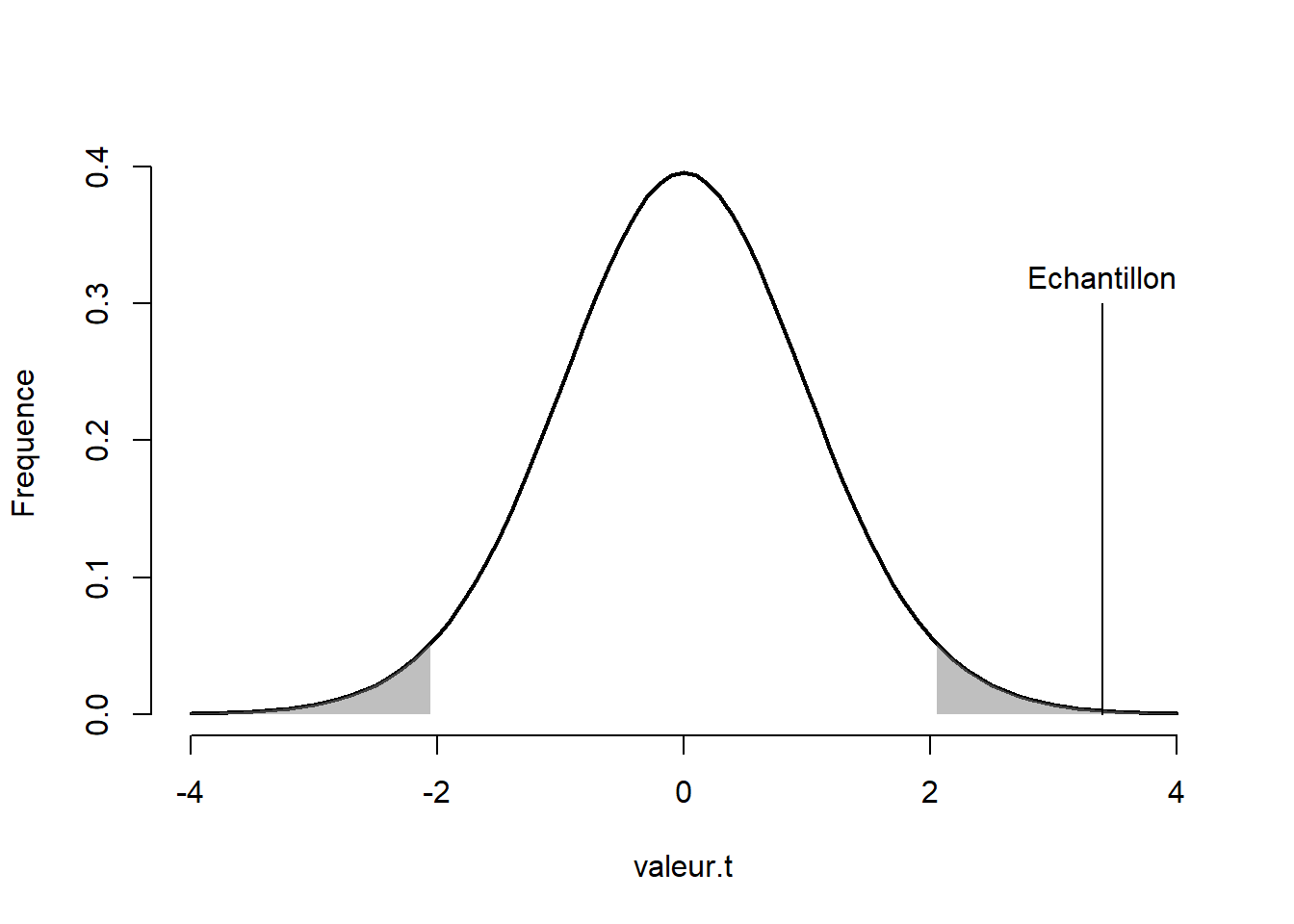
Figure 11.1: Valeur-\(t\) de la différence de moyenne sur la distribution-\(t\)

La Figure 11.1 illustre où se situe la moyenne de l’échantillon par rapport à la distribution d’échantillonnage de l’hypothèse nulle. Comme la valeur se retrouve dans la zone de rejet ou, de façon équivalente, la valeur-\(p\) est plus petite que la valeur \(\alpha\) fixée à .05, on rejette l’hypothèse nulle, il y a vraisemblablement une différence entre les groupes. C’est bien l’intention derrière la création des données.

11.1.2 Rapporter un test-\(t\) indépendant

Voici comment il est possible de rapporter les résultats. La syntaxe pour commander l’analyse est la suivante si les groupes sont dans deux vecteurs séparés.

t.test(gr0, gr1) # Absence de l'argument var.equal = TRUE
> 
>   Welch Two Sample t-test
> 
> data:  gr0 and gr1
> t = 3, df = 27, p-value = 0.002
> alternative hypothesis: true difference in means is not equal to 0
> 95 percent confidence interval:
>  0.539 2.182
> sample estimates:
> mean of x mean of y 
>     1.332    -0.029

Il est également possible d’utiliser la formule si, dans le jeu de données, une variable permet de distinguer les deux groupes et que la variable continue (variable à comparer) se trouve dans une seule variable.

# Mettre les variables en jeu de données
jd.ti <- data.frame(VD = c(gr0, gr1),
                    VI = x1)
t.test(VD ~ VI, data = jd.ti)
> 
>   Welch Two Sample t-test
> 
> data:  VD by VI
> t = 3, df = 27, p-value = 0.002
> alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
> 95 percent confidence interval:
>  0.539 2.182
> sample estimates:
> mean in group 0 mean in group 1 
>           1.332          -0.029

La présente étude compare deux groupes sur une échelle de mesure psychologique. Le test-\(t\) indépendant suggère que la différence entre les groupes est significative, \(t(26.912) =3.398, p = 0.002\).

11.1.3 Le test-\(t\) dépendant

Un autre test-\(t\) est celui permettant de comparer deux de temps de mesure sur les mêmes participants. L’hypothèse est de vérifier si \(\mu_1 = \mu_2\), soit la moyenne du temps 1 est égale à la moyenne du temps 2. Une habile manipulation mathématique permet de poser cette hypothèse en hypothèse nulle, \(\mu_1-\mu_2=0\). Il est intéressant de noter que la différence entre deux variables est normalement distribuée si la variance est connue ou distribuée en \(t\) si la variance est inconnue.

Ce test est utile lorsqu’il faut tester si les participants se sont améliorés ou détériorés entre deux temps de mesure. Pour calculer la valeur-\(t\),

\[ t_{dl_1} = \frac{\bar{x_1}-\bar{x_2}}{\sigma_d/\sqrt{n}} \]

avec \(n-1\) degrés de liberté à cause de l’estimation de l’écart type des différences. Les étapes subséquentes sont identiques au test-\(t\) à groupe unique.

testt.dep <- function(temps1, temps2){
  # Temps est une variable continue mesurée 
  # à deux occasions auprès des mêmes participants
  
  # Calculer la différence
  difference <- temps1 - temps2
  dbar <- mean(difference) # La moyenne des différences
  dvar <- var(difference)  # L'écart type des différences
  n <- length(difference)  # Taille d'échantillon
  
  # Valeur-t, degrés de liberté et valeur-p
  vt <- (dbar) / sqrt(dvar / n)
  dl <- n - 1                   
  vp <- (1 - pt(abs(vt), df = dl)) * 2 
  statistique <- list(valeur.t = vt, dl = dl, valeur.p = vp)
  return(statistique)
}

Pour créer le jeu de données, les étapes sont similaires au test-\(t\) indépendant pour des temps de mesure indépendants (sans corrélation) où seules les populations des temps de mesure sont définis. Il est possible de spécifier une corrélation entre les deux de mesures. Cela sera introduit dans la section La corrélation.

Dans le jeu de données suivant, 25 personnes sont mesurées à deux temps de reprises. Il n’y a pas de corrélation entre les temps de mesure. La variance des temps de mesure est de 1. La différence de moyenne est de 2. La syntaxe simule la situation suivante, le temps1 correspond à la mesure initiale et difference correspond à la différence entre les temps de mesure. La somme de ces deux scores donnent la mesure au temps2. Cela montre assez simplement que la différence entre temps2 - temps1 permet de retrouver le vecteur de difference.

# Un exemple de jeu de données
set.seed(148)
temps1 <- rnorm(n = 25, mean = 0, sd = 2)
difference <- rnorm(n = 25, mean = 2, sd = 2)
temps2 <- temps1 + difference

La fonction base de R est encore t.test(), mais il faudra spécifier l’argument paired = TRUE pour commander un test apparié (une autre appellation pour un test-\(t\) dépendant).

t.test(temps1, temps2, paired = TRUE)
> 
>   Paired t-test
> 
> data:  temps1 and temps2
> t = -3, df = 24, p-value = 0.004
> alternative hypothesis: true mean difference is not equal to 0
> 95 percent confidence interval:
>  -2.172 -0.465
> sample estimates:
> mean difference 
>           -1.32
testt.dep(temps1, temps2)
> $valeur.t
> [1] -3.19
> 
> $dl
> [1] 24
> 
> $valeur.p
> [1] 0.00395

Les sorties sont identiques.

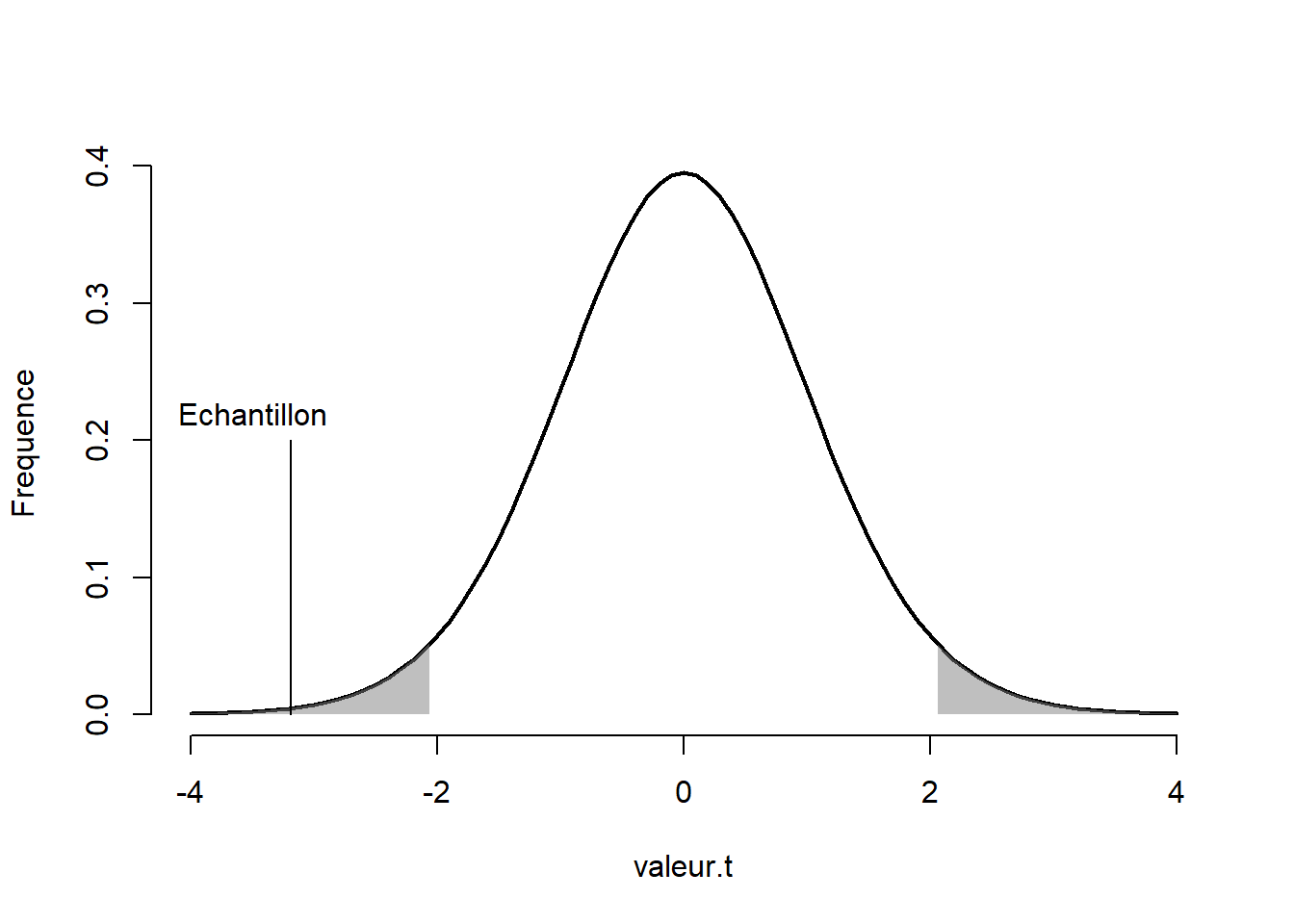
Figure 11.2: Valeur-\(t\) de moyenne de différences sur la distribution-\(t\)

La Figure 11.2 montre où se situe la différence de moyenne par rapport à la distribution d’échantillonnage de l’hypothèse nulle. Comme la valeur se retrouve dans la valeur-\(p\) est plus petite que la valeur \(\alpha\) fixée à .05, on rejette l’hypothèse nulle; il y a vraisemblablement une différence entre les temps de mesure, ce qui était l’intention derrière la création des données.

11.1.3.1 Autres syntaxes possibles

Il y a plusieurs façons de réaliser un test-\(t\) dépendant. La première option est celle décrite précédemment.

# Technique précédent avec deux vecteurs
t.test(x = temps1, y = temps2, paired = TRUE)
> 
>   Paired t-test
> 
> data:  temps1 and temps2
> t = -3, df = 24, p-value = 0.004
> alternative hypothesis: true mean difference is not equal to 0
> 95 percent confidence interval:
>  -2.172 -0.465
> sample estimates:
> mean difference 
>           -1.32

La second option utilise la formule et le jeu de données. La fonction Pair() n’a que seule objectif d’informer la fonction t.test() que les vecteurs qu’elle inclut sont pairés, ce qui permet d’utiliser la formule Pair(temps1, temps2) ~ 1.

# Avec la formule et les variables dans le même jeu de données
jd.td <- data.frame(temps1 = temps1,
                    temps2 = temps2)
t.test(Pair(temps1, temps2) ~ 1, data = jd.td)
> 
>   Paired t-test
> 
> data:  Pair(temps1, temps2)
> t = -3, df = 24, p-value = 0.004
> alternative hypothesis: true mean difference is not equal to 0
> 95 percent confidence interval:
>  -2.172 -0.465
> sample estimates:
> mean difference 
>           -1.32

Pour la troisième option, comme l’équation sur le test-\(t\) dépendant le suggère, un test-\(t\) dépendant revient à faire un test-\(t\) à échantillon unique avec la différence entre les deux temps de mesure.

# Avec la différence des deux vecteurs
t.test(temps2 - temps1)
> 
>   One Sample t-test
> 
> data:  temps2 - temps1
> t = 3, df = 24, p-value = 0.004
> alternative hypothesis: true mean is not equal to 0
> 95 percent confidence interval:
>  0.465 2.172
> sample estimates:
> mean of x 
>      1.32

Une quatrième option, si le temps est une colonne dans le jeu de données, alors le même style de formule peut être utilisé comme Le test-\(t\) indépendant toujours en indiquant paired = TRUE.

# Avec la formule et les variables dans le même jeu de données
# Le temps est une seule variable
jd.td2 <- data.frame(mesure = c(temps1, temps2),
               temps = rep(1:2, each = 25))
t.test(mesure ~ temps, data = jd.td2, paired = TRUE)
> 
>   Paired t-test
> 
> data:  mesure by temps
> t = -3, df = 24, p-value = 0.004
> alternative hypothesis: true mean difference is not equal to 0
> 95 percent confidence interval:
>  -2.172 -0.465
> sample estimates:
> mean difference 
>           -1.32

11.1.4 Rapporter un test-\(t\) dépendant

Voici comment rapporter dans un article.

Un groupe de participants est mesuré à deux reprises sur une même mesure psychologique. Le test-\(t\) dépendant suggère que la différence entre les temps de mesure est significative, \(t(24) =-3.188, p = 0.002\).

11.2 L’association linéaire

11.2.1 La covariance

La covariance représente une mesure du degré auquel une variable augmente lorsque l’autre augmente. Elle correspond au produit moyen entre deux variables centrées (dont les moyennes sont soustraites). On retrouve la covariance sous la forme de l’équation (11.4).

\[\begin{equation} \text{cov}_{xy} = \sigma_{xy}=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) \tag{11.4} \end{equation}\]

La covariance est une extension multivariée de la variance. La variance est le produit d’une variable centrée avec elle-même (le carré de la variable), \[\sigma^2=\frac{1}{n-1}\sum_{i=1}^nx_ix_i\].

En transformant \(x\) et \(y\) pour qu’elles soient centrées, l’aspect de produit entre les deux variables devient évident dans l’expression de la covariance. \[\text{cov}_{xy} = \frac{1}{n-1}\sum_{i=1}^nxy\] La programmation de la covariance peut se traduire ainsi.

covariance <- function(x, y){
  # X est une data.frame ou matrice de n sujets par p variables
  n <- length(x)
  # centrer variables
  xc <- x - mean(x)
  yc <- y - mean(y)
  prod.xy <- xc * yc
  cov.xy <- sum(prod.xy) / (n-1)
  return(cov.xy)
}

La fonction de base cov() est plus efficace (plus robuste et plus simple) que la fonction maison précédente. La fonction cov() peut tenir compte de plus de deux variables. La covariance indique la direction de la covariation entre les deux variables, positives ou négatives, mais n’indique pas la force de la relation. Bien qu’une covariance de 0 indique l’absence de colinéarité, une covariance de 120 n’est pas nécessairement plus forte qu’une covariance de 1. La mesure est intrinsèquement influencée par les unités l’échelle de mesure. Il serait aberrant de considérer le système métrique comme moins efficace, car ces mesures sont moins variables que les mesures impériales. (Il y a plusieurs raisons de préférer le système métrique, mais ce n’en est pas une!)

11.2.2 La corrélation

La corrélation représente le degré d’association linéaire entre deux variables. Une façon simple de concevoir la corrélation est comme une covariance standardisée. Elle varie entre -1 et 1, ces deux dernières valeurs impliquant, respectivement, une relation parfaitement négative et positive entre les deux variables. En plus d’indiquer la direction de la relation, la corrélation suggère une force à ce lien. Lorsque la valeur de la corrélation est nulle, \(r=0\), un diagramme de dispersion ne montre qu’un nuage de point épars (sans structure). Plus la corrélation augmente (en terme absolu), plus le nuage tends vers une ligne droite. La Figure 11.3 montre différentes valeurs de corrélation et un exemple de nuage de points qui lui est associé.

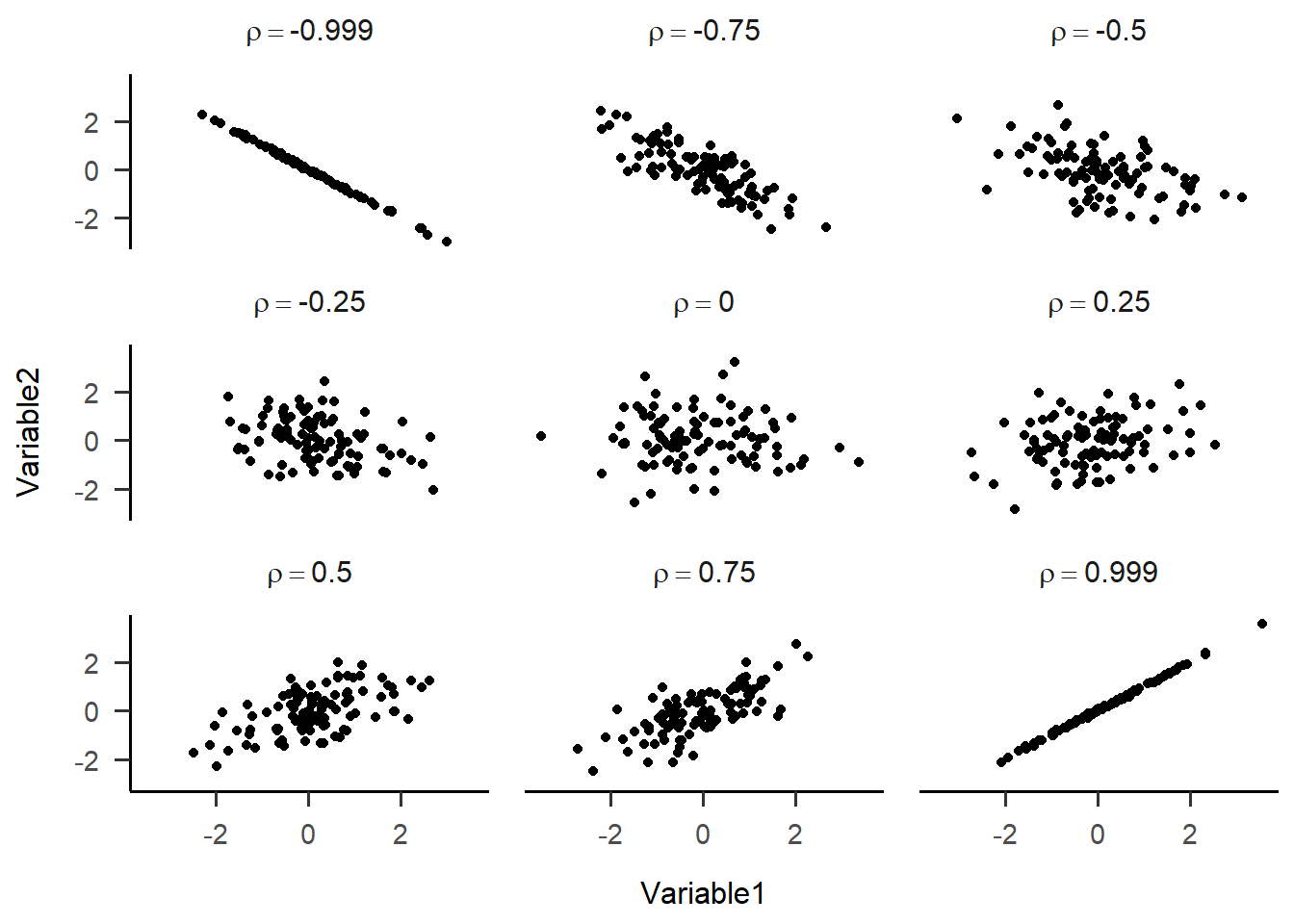
Figure 11.3: Illustrations de diagrammes de dispersion associé en fonction de corrélations

En statistiques, la corrélation est souvent représentée par la lettre grecque \(\rho\) (rho) ou l’usuel \(r\) lorsqu’il s’agit d’une estimation à partir d’un échantillon.

Il y a plusieurs méthodes pour calculer la corrélation. Une première est de considérer la corrélation comme le produit de variables standardisées (autrement dit, score-\(z\)). Pour la covariance, la moyenne était soustraite de la variable, c’est-à-dire des variables centrées. Pour la corrélation, on divise pas l’écart type également pour obtenir des variables standardisées.

En admettant que \(x\) et \(y\) sont déjà standardisée, \(z_x,z_y\), comme c’était le cas pour la covariance, l’aspect de produit entre les deux variables est conservé. \[\text{cor}_{xy} = r_{xy}= \frac{1}{n-1}\sum_{i=1}^nz_xz_y\]

Il est possible de calculer directement la corrélation à partir de la covariance, soit en divisant par le produit des écarts types des variables.

\[r_{xy} = \frac{\text{cov}_{xy}}{\sigma_x\sigma_y}\]

Voici trois options de programmation de la corrélation. La première et la deuxième sont basées sur la covariance. Dans la première, la covariance est calculée de nouveau dans la fonction. La deuxième quant à elle profite avantageusement de l’existence d’une fonction maison qui calcule directement la covariance. La troisième recourt au produit de variables standardisées.

# Option 1 : Calcul complet
correlation1 <- function(x, y){
  
  # La taille d'échantillon
  n <- length(x)
  
  # Centrer les variables
  xc <- x - mean(x)
  yc <- y - mean(y)
  
  # Produit des variables
  prod.xy <- xc * yc
  
  # La somme des produits divisée par n - 1
  cov.xy <- sum(prod.xy) / (n - 1)  # La covariance
  
  # Diviser par les écarts types
  cor.xy <- cov.xy / (sd(x) * sd(y))
  
  return(cor.xy)
}

# Option 2 : Basé sur la covariance
correlation2 <- function(x, y){
  
  # Calculer la covariance
  cov.xy <- covariance(x,y)
  
  # Diviser par les écarts types
  cor.xy <- cov.xy / (sd(x) * sd(y))
  return(cor.xy)
}

# Option 3 : Basé sur des variables standardisées
correlation3 <- function(x, y){
  
  # La taille d'échantillon
  n <- length(x)
  
  # Centrer et réduire les variables
  xs <- (x - mean(x)) / sd(x)
  ys <- (y - mean(y)) / sd(y)
  
  # La somme des produits divisé par n - 1
  cor.xy <- sum(xs * ys)/(n - 1)
  
  return(cor.xy)
}

Évidemment, R possède une fonction de base pour le calcul d’une corrélation entre deux variables ou d’une matrice de corrélation (à partir d’un jeu de données de deux variables ou plus). Il s’agit de cor(). Ces trois fonctions maison en plus de la fonction R sont comparées ci-dessous. Pour ce faire, un jeu de données est créé possédant les caractéristiques désirées. Dans ce cas-ci, la taille d’échantillon est fixée à \(n=10000\) pour assurer une bonne précision dans l’échantillon et une corrélation \(r=.7\).

Une façon simple de produire des données à partir d’une matrice de corrélation (ou de covariance) est d’utiliser la fonction mvrnorm() du package MASS. Elle évite pour l’instant d’introduire les manipulations mathématiques nécessaires (ce sera donc pour l’instant l’une de ces boîtes noires ayant la confiance de l’utilisateur, mais élucider dans le chapitre Créer).

La fonction mvrnorm() pour MultiVariate Random NORMmal nécessite trois arguments :

• la taille d’échantillon n;

• les moyennes mu des \(p\) variables, et;

• la matrice de covariance Sigma (la corrélation est un cas particulier de la covariance où les variables sont standardisées).

Le lecteur avisé aura noté la ressemblance de nomenclature entre mvrnorm() (multivariée) et rnorm() (univariée). Enfin, la dernière étape est de produire une matrice de covariance \(p \times p\). La fonction matrix() prend une variable de données, dans cet exemple , c(1, r, r, 1) qu’elle répartit ligne par colonne (voir Créer une matrice. Comme \(p=2\), cela crée une matrice \(2 \times 2\).

# Pour la reproductibilité
set.seed(820)

# Taille d'échantillon importante pour réduire l'erreur d'échantillonnage
n <- 10000

# La corrélation désirée
r <- .70

# Création d'une matrice de corrélation
R <- matrix(c(1, r, r, 1), nrow = 2, ncol = 2)

# Création des données 
donnees <- data.frame(MASS::mvrnorm(n = n, 
                                    mu = c(0,0), 
                                    Sigma = R))
colnames(donnees) <- c("x", "y") # Ajouter des noms de colonnes

# Voici la matrice de corrélation
R
>      [,1] [,2]
> [1,]  1.0  0.7
> [2,]  0.7  1.0

# Voici une visualisation partielle des données
head(donnees)
>        x      y
> 1  0.635  0.914
> 2 -0.193  0.360
> 3 -0.602 -1.213
> 4 -0.841 -0.986
> 5 -0.105 -1.771
> 6 -2.147 -1.590

# Vérifications des variables
mean(donnees$x); mean(donnees$y); sd(donnees$x); sd(donnees$y)
> [1] -0.00578
> [1] -0.00531
> [1] 0.999
> [1] 1.01

# Les résultats sont près des attentes
# Vérifications de la corrélations
cor(donnees$x, donnees$y)
> [1] 0.699
correlation1(donnees$x, donnees$y)
> [1] 0.699
correlation2(donnees$x, donnees$y)
> [1] 0.699
correlation3(donnees$x, donnees$y)
> [1] 0.699

Les résultats sont près des attentes et identiques.

Pour tester la probabilité d’obtenir cette valeur, la corrélation \(r\) peut se transformer monotonement en valeur-\(t\) avec l’équation (11.5), ce qui permet de calculer des valeurs-\(p\).

\[\begin{equation} t_{n-2} = \frac{r}{(\frac{\sqrt{1-r^2}}{\sqrt{n-2}})} \tag{11.5} \end{equation}\]

L’équation (11.5) se traduit simplement en code R.

# Création d'une matrice de corrélation 
# Il pourrait également s'agir d'un vecteur ou d'un scalaire.
r <- matrix(c( 1, .5, .4,
               .5,  1, .3,
               .4, .3,  1), 
            nrow = 3, ncol = 3)

# Nombre d'unités (valeur arbitraire ici)
n <- 10

# Valeurs-t
vt <- r * sqrt(n - 2) / sqrt(1 - r ^ 2)

# Valeurs-p
vp <- (1 - pt(abs(vt), df = n - 2)) * 2
vt ; vp
>      [,1]  [,2]  [,3]
> [1,]  Inf 1.633 1.234
> [2,] 1.63   Inf 0.889
> [3,] 1.23 0.889   Inf
>       [,1]  [,2]  [,3]
> [1,] 0.000 0.141 0.252
> [2,] 0.141 0.000 0.400
> [3,] 0.252 0.400 0.000

Dans le code ci-dessous, l’équation (11.5) précédente est subtilement réarrangée pour être plus simple et élégante quoiqu’équivalente.

\[\begin{equation} t_{n-2} = \frac{r}{(\frac{\sqrt{1-r^2}}{\sqrt{n-2}})} = \frac{r\sqrt{n-2}}{\sqrt{1-r^2}} \tag{11.6} \end{equation}\]

L’équation (11.5) a l’avantage de montrer la relation entre l’estimateur et l’erreur type alors que l’équation (11.6) est moins encombrante.

11.2.3 Rapporter une corrélation

Voici comment rapporter la corrélation dans un article. Plusieurs options sont possibles. Pour une seule corrélation, R permet d’obtenir la corrélation et la valeur-\(p\) avec la fonction cor.test(). Il est possible de rédiger la syntaxe ainsi.

cor.test(donnees$x, donnees$y)

ou encore comme ceci.

cor.test(~ y + x, data = donnees)
> 
>   Pearson's product-moment correlation
> 
> data:  y and x
> t = 98, df = 9998, p-value <2e-16
> alternative hypothesis: true correlation is not equal to 0
> 95 percent confidence interval:
>  0.689 0.709
> sample estimates:
>   cor 
> 0.699

En général, la matrice corrélation complète est intéressante à rapporter. Cela se fait rapidement et simplement avec la fonction cor(). Toutefois, elle ne rapporte pas les valeurs-\(p\) et n’est pas agrémentée d’étoiles scintillantes. Plusieurs packages et fonctions sont envisageables, mais psych avec sa fonction corr.test est l’une des plus pertinentes. Voici un exemple avec le jeu de données mtcars (disponible dans R de base).

psych::corr.test(mtcars)
> Call:psych::corr.test(x = mtcars)
> Correlation matrix 
>        mpg   cyl  disp    hp  drat    wt  qsec    vs    am
> mpg   1.00 -0.85 -0.85 -0.78  0.68 -0.87  0.42  0.66  0.60
> cyl  -0.85  1.00  0.90  0.83 -0.70  0.78 -0.59 -0.81 -0.52
> disp -0.85  0.90  1.00  0.79 -0.71  0.89 -0.43 -0.71 -0.59
> hp   -0.78  0.83  0.79  1.00 -0.45  0.66 -0.71 -0.72 -0.24
> drat  0.68 -0.70 -0.71 -0.45  1.00 -0.71  0.09  0.44  0.71
> wt   -0.87  0.78  0.89  0.66 -0.71  1.00 -0.17 -0.55 -0.69
> qsec  0.42 -0.59 -0.43 -0.71  0.09 -0.17  1.00  0.74 -0.23
> vs    0.66 -0.81 -0.71 -0.72  0.44 -0.55  0.74  1.00  0.17
> am    0.60 -0.52 -0.59 -0.24  0.71 -0.69 -0.23  0.17  1.00
> gear  0.48 -0.49 -0.56 -0.13  0.70 -0.58 -0.21  0.21  0.79
> carb -0.55  0.53  0.39  0.75 -0.09  0.43 -0.66 -0.57  0.06
>       gear  carb
> mpg   0.48 -0.55
> cyl  -0.49  0.53
> disp -0.56  0.39
> hp   -0.13  0.75
> drat  0.70 -0.09
> wt   -0.58  0.43
> qsec -0.21 -0.66
> vs    0.21 -0.57
> am    0.79  0.06
> gear  1.00  0.27
> carb  0.27  1.00
> Sample Size 
> [1] 32
> Probability values (Entries above the diagonal are adjusted for multiple tests.) 
>       mpg cyl disp   hp drat   wt qsec   vs   am gear carb
> mpg  0.00   0 0.00 0.00 0.00 0.00 0.22 0.00 0.01 0.10 0.02
> cyl  0.00   0 0.00 0.00 0.00 0.00 0.01 0.00 0.04 0.08 0.04
> disp 0.00   0 0.00 0.00 0.00 0.00 0.20 0.00 0.01 0.02 0.30
> hp   0.00   0 0.00 0.00 0.17 0.00 0.00 0.00 1.00 1.00 0.00
> drat 0.00   0 0.00 0.01 0.00 0.00 1.00 0.19 0.00 0.00 1.00
> wt   0.00   0 0.00 0.00 0.00 0.00 1.00 0.02 0.00 0.01 0.20
> qsec 0.02   0 0.01 0.00 0.62 0.34 0.00 0.00 1.00 1.00 0.00
> vs   0.00   0 0.00 0.00 0.01 0.00 0.00 0.00 1.00 1.00 0.02
> am   0.00   0 0.00 0.18 0.00 0.00 0.21 0.36 0.00 0.00 1.00
> gear 0.01   0 0.00 0.49 0.00 0.00 0.24 0.26 0.00 0.00 1.00
> carb 0.00   0 0.03 0.00 0.62 0.01 0.00 0.00 0.75 0.13 0.00
> 
>  To see confidence intervals of the correlations, print with the short=FALSE option

La syntaxe retourne les corrélations, la taille d’échantillon et les valeurs-\(p\). La sortie contient encore plus d’informations, mais elle n’imprime que les usuelles. Il ne reste qu’à rédiger les corrélations les plus pertinents à rapporter (selon la théorie du domaine concerné).

La matrice de corrélation des variables présentés. Parmi les corrélations d’intérêt, un lien remarquable est celui entre qsec et mpg qui est significatif, \(r(10) = 0.42, p\ =\ = 0.42\).

11.3 Les données nominales

Jusqu’à présent, deux types d’association de données ont été présenté : une variable nominale (identifiant des groupes) avec une variable continue (différences de moyenne) et deux variables continues (association linéaire). Dans cette section, l’association entre deux variables nominales est présentée. Une façon de représenter l’association entre deux variables nominales est le tableau de contingence, soit l’illustration d’une distribution d’une variable (en ligne) pour chaque catégorie de l’autre (en colonne). En voici, un exemple.

Table 11.1: Tableau de contingence de la relation entre posséder une voiture et le climatoscepticisme

Climatosceptique	Voiture
	non	oui
non	87	104
oui	7	52

Le tableau 11.1 présente deux variables nominales (climatosceptique, à la verticale, et posséder une voiture, à l’horizontale) ayant chacune deux catégories (oui et non). Il montre les proportions observées. Ces variables sont-elles associées? Pour traiter cette question, les proportions attendues jouent un rôle crucial. En fait, l’hypothèse nulle sous la table de contingence postule que toutes les proportions du tableau de contingence sont indépendantes. Mathématiquement, il s’agit de postuler que les proportions d’une variable (en ligne ou en colonne) n’influencent pas celles de l’autre variable. Pour obtenir les proportions théoriques, les totaux des lignes et colonnes sont calculés ainsi que le grand total. La fréquence attendue d’une cellule est obtenue en calculant, pour chaque cellule, le produit de sa colonne et de sa ligne respective divisé par le grand total.

\[\begin{equation} t_{ij} = \frac{\text{total}_i \times \text{total}_j}{\sum \text{total}} \tag{11.7} \end{equation}\]

L’équation (11.7) ci-dessus illustre l’idée sous-jacente à la proportion attendue, \(t\) d’une cellule de ligne, \(i\), et colonne \(j\).

Table 11.2: Tableau de contingence étendu avec les totaux

Climatosceptique	Voiture		Total
	non	oui
non	87	104	191
oui	7	52	59
Total	94	156	250

11.3.1 Le \(\chi^2\) pour table de contingence

Maintenant que la question statistique et que l’hypothèse nulle sont posées, comment mesurer le degré selon lequel les données s’écartent des attentes théoriques. Le \(\chi^2\) (khi-carré) permet de calculer une telle mesure. Le \(\chi^2\) correspond à la distance entre une valeur observée et théorique au carré, pondérée par la valeur théorique. \[ \chi^2_v = \sum_{i=1}^{l}\sum_{j=1}^c(\frac{(o_{ij}-t_{ij})^2}{t_{ij}})\] où \(o\) correspond aux valeurs observées, \(t\) réfère aux valeurs théoriques, \(v\) représente les degrés de liberté et \(i\) et \(j\) les lignes et colonnes respectivement. Le degré de liberté est \[v = (n_{\text{ligne}}-1)(n_{\text{colonne}}-1)\]

Si l’hypothèse nulle est vraie, les valeurs observées et théoriques devraient être très près. Le carré permet de calculer une distance euclidienne et le dénominateur pondère la distance. Comme l’analyse de variance, le test de \(\chi^2\) pour table de contingence est global, il n’informe pas d’où provient la dépendance, mais bien s’il y a au moins une dépendance.

khicarre <- function(obs){
  # Obs est une table de contingence
  # Somme colonne
  SC <- as.matrix(colSums(obs))
  # Somme ligne
  SL <- as.matrix(rowSums(obs))
  # Grand total
  TT <- sum(obs)
  # Proportion théoriques
  theo <- SL %*% t(SC) / TT
  # khi carré
  khi2 <- sum((obs - theo) ^ 2 / theo)
  dl <- (length(SL) - 1) * (length(SC) - 1)
  vp <- 1 - pchisq(khi2, dl)
  # Sortie
  statistiques <- list(khi2 = khi2, dl = dl, valeur.p = vp)
  return(statistiques)
}

Il y a plusieurs techniques pour créer une base de données, l’essentiel étant de lier les proportions désirées. Ici, une variable sexe est créée avec 50-50% de chance d’être l’un ou l’autre sexe. Par la suite, une proportion différente liée au sexe est utilisée pour générer la fréquence de consommation de tabac. La syntaxe sert principalement à identifier les valeurs homme et femme de la première variable pour en associer une valeur tabac.

set.seed(54)
n <- 100

# Première variable
sexe <- sample(c("homme","femme"), 
               size = n, 
               replace = TRUE, 
               prob = c(.5,.5))
tabac <- rep(0, 100)

# Proportions conditionnelles
tabac[sexe == "femme"] <- sample(c("fumeur","non-fumeur"), 
                                 size = sum(sexe == "femme"), 
                                 replace = TRUE, 
                                 prob = c(.2,.8))

tabac[sexe == "homme"] <- sample(c("fumeur","non-fumeur"), 
                                 size = sum(sexe == "homme"), 
                                 replace = TRUE, 
                                 prob = c(.1,.9))
#base données
donnees <- data.frame(sexe, tabac)
table(donnees)
>        tabac
> sexe    fumeur non-fumeur
>   femme      8         38
>   homme      4         50

La fonction table() de R génère une table de contingence. La fonction maison et deux méthodes de base R sont présentées et produisent les mêmes résultats pour le \(\chi^2\). Un autre, le test exact de Fisher est également présenté. Celui-ci est plus robuste, mais peut requérir plus intensive des ressources de l’ordinateur pour les grosses tables de contingences.

Le test du \(\chi^2\) est sujet à certains problèmes qu’il est important de considérer sans quoi l’interprétation peut être faussée. Si la taille d’échantillon (le nombre d’unités d’observation observées est trop faible), alors le test est biaisé. Par exemple, trois lancers de pile ou face ne sont pas suffisants pour tester une hypothèse de khi-carré, le nombre de résultats différents est de 2, ce qui ne donne pas une approximation satisfaisante de la distribution d’échantillonnage. La convention est de dire qu’une fréquence théorique est trop petite si elle est plus petite que 5. Si ce n’est pas le cas, des corrections ou d’autres options doivent être considérées.

Dans le présent exemple, bien que les fréquences attendues respectent les critères usuels, il peut être utile d’envisager un test plus robuste comme le test exact de Fisher ou le \(\chi^2\) avec correction de continuité. Le premier se commande avec la fonction fisher.test() et le second est la fonction par défaut de chisq.test(). C’est deux fonctions prennet comme argument une table de contigence (la sortir de table()) ou deux variables nominales. Pour montrer l’équivalence entre la fonction chisq.test() et la fonction maison, l’option de correction est désactivée avec l’argument correct = FALSE.

# Table de contingence
TC <- table(donnees)
# Fonction maison
khicarre(TC)
> $khi2
> [1] 2.34
> 
> $dl
> [1] 1
> 
> $valeur.p
> [1] 0.126

# Fonction de base
summary(TC)
> Number of cases in table: 100 
> Number of factors: 2 
> Test for independence of all factors:
>   Chisq = 2.3, df = 1, p-value = 0.1

# Autre fonction de base
resultat <- chisq.test(TC, correct = FALSE)
# ou encore
resultat <- chisq.test(donnees$sexe, donnees$tabac, correct = FALSE)
# Leur sortie
resultat
> 
>   Pearson's Chi-squared test
> 
> data:  donnees$sexe and donnees$tabac
> X-squared = 2, df = 1, p-value = 0.1

# Et pour plus de précision...
resultat$statistic
> X-squared 
>      2.34
resultat$p.value
> [1] 0.126

# Le test exact de Fisher
resultat.fisher <- fisher.test(TC)
# ou encore
resultat.fisher <- fisher.test(donnees$sexe, donnees$tabac)
# Leur sortie
resultat.fisher
> 
>   Fisher's Exact Test for Count Data
> 
> data:  donnees$sexe and donnees$tabac
> p-value = 0.2
> alternative hypothesis: true odds ratio is not equal to 1
> 95 percent confidence interval:
>   0.641 12.731
> sample estimates:
> odds ratio 
>       2.61
resultat.fisher$p.value
> [1] 0.216

11.3.2 Rapporter un \(\chi^2\)

Voici comment rapporter un test de \(\chi^2\) dans un article. Comme il a été vu ci-haut, plusieurs options sont possibles

# Pour le khi carré de Pearson
chisq.test(donnees$sexe, donnees$tabac, correct = FALSE)
> 
>   Pearson's Chi-squared test
> 
> data:  donnees$sexe and donnees$tabac
> X-squared = 2, df = 1, p-value = 0.1

# Pour le test exact de Fisher
fisher.test(donnees$sexe, donnees$tabac)
> 
>   Fisher's Exact Test for Count Data
> 
> data:  donnees$sexe and donnees$tabac
> p-value = 0.2
> alternative hypothesis: true odds ratio is not equal to 1
> 95 percent confidence interval:
>   0.641 12.731
> sample estimates:
> odds ratio 
>       2.61

La relation entre le sexe et le consommation de tabac est investiguée. Il appert que cette relation n’est pas statistiquement significative avec une seuil \(\alpha = .05\), \(chi^2(1) = 2.345\), \(p = 0.126\). Le test exact de Fisher est calculé également et, pareillement, ne rejette pas l’hypothèse nulle, \(p =0.216\).

11.3.3 La correction de Yates

Même si c’est généralement le test classique de Pearson qui est utilisé, le \(\chi^2\) avec correction de Yates, l’option par défaut de chisq.test(), est préférable. C’est un test un peu plus conservateur qui compense pour les déviations de la distribution de probabilité théorique. La correction consiste à faire la différence absolue entre la fréquence observée et théorique, puis de soustraire \(\frac{1}{2}\), ce qui est représentée par l’équation suivante.

\[ \chi^2_v = \sum_{i=1}^{l}\sum_{j=1}^c(\frac{(|o_{ij}-t_{ij}|-\frac{1}{2})^2}{t_{ij}})\]