21 Confirmer
La modélisation par équations structurelles permet de combiner toutes les analyses qui ont été vues jusqu’à maintenant que ce soit, la modération, la médiation, la régression et les analyses factorielles. Ce chapitre insiste sur l’aspect confirmatoire des analyses statistiques. Autrement dit, la modélisation par équations structurelles ne devrait pas découvrir des modèles, mais bien à tester et vérifier. Pour rappel, c’était déjà le cas pour la modération et la médiation.
Pour réaliser des modèles par équations structurelles, le package lavaan est le plus recommandé. Il se distingue par sa flexibilité et sa simplicité d’utilisation, permettant aux utilisateurs de spécifier et de tester des modèles compliqués avec un langage syntaxique clair et intuitif qui rappelle Mplus (Muthén & Muthén, 1998-2017). Parmi ses principales qualités, lavaan offre une large gamme de fonctionnalités pour l’estimation des modèles, les ajustements, et la comparaison des modèles, tout en supportant les analyses confirmatoires et exploratoires. Sa capacité à gérer les modèles avec des variables latentes, ses options de diagnostic détaillées et ses outils de visualisation font de lavaan un outil essentiel pour les expérimentateurs et ulisistaeur souhaitant mener des modèles par équations structurelles robustes et fiables.
Comme pour tous les packages, il faut d’abord installer et appeler le programme avant de l’utiliseré
21.1 Spécifier un modèle
La première étape d’un modèle avec lavaan est d’écrire un modèle. Comme il s’agit de multiple formules, il ne sera pas d’utiliser le traditionnel ~. Un modèle d’équation structurelle de lavaan se compose d’une seule chaîne de caractères commençant et finissant par des guillemets anglophone comme model <- "les équations" et qui contient toutes les équations. Il est important que chaque équation ait sa propre ligne. Voici une liste d’opérateur les plus commun.
~signifie prédit par, commey ~ x + m~~se traduit par est lié à, comme une covariancex ~~ y=~est se mesure de, commeF1 =~ i1 + i2 + i3*nomme ou fixe un paramètre selon le préfixe, par exemple,y ~ a*xpermet d’utiliser le coefficient de régression lié àx,y ~ .5*xfixe le coefficient à .5 ou. sia(le libellé) est utilisé à plusieurs endroits, cela contraint la valeur à être identiquer pour les deux équations.:=définit un paramètre, par exemple, s’il faut la somme ou le produit de différents coefficients.
Une fois le modèle assigné dans une variable, les fonctions sem() et cfa() pourront être utilisées pour tester le modèle aux données. Les deux sont virtuellement identiques.
21.2 Les fonctions
21.2.1 Les indices d’ajustement
Une fois l’analyse l’analyse, l’utilisateur peut regarder les indices d’ajustement. Il est recommandé de rapporter le \(\chi^2\) avec sa valeur-\(p\) et ses degrés de liberté ainsi que l’indice comparatif d’ajustement (CFI), l’indice de Tucker-Lewis (TLI), l’erreur quadratique moyenne d’approximation (RMSEA) et le résidu quadratique moyen standardiséé (SRMR).
Dans le contexte des modèles d’équations structurelles, le \(\chi^2\) est un indice classique de la qualité de l’ajustement du modèle aux données observées. Il compare la matrice de covariance observée des données à la matrice de covariance prédite par le modèle. Le but est de déterminer si les différences entre ces deux matrices peuvent être attribuées à des variations aléatoires. Une valeur-\(p\) supérieure à 0.05 (non significative) suggère que le modèle s’ajuste bien aux données. Le \(\chi^2\) est très sensible à la taille de l’échantillon. Pour des échantillons très grands, de petites différences peuvent produire une valeur significative, suggérant à tort un mauvais ajustement. Pareillement, pour les modèles avec de nombreux paramètres, il peut souvent indiquer un mauvais ajustement en raison de l’accumulation d’erreurs.
Le CFI est un indice utilisé dans la modélisation par équations structurelles (SEM) pour évaluer la qualité de l’ajustement d’un modèle par rapport à un modèle de référence. Il compare le modèle testé à un modèle nul (ou indépendant) où il n’existe aucune relation entre les variables observées. Le CFI varie entre 0 et 1, avec des valeurs plus proches de 1 indiquant un meilleur ajustement. En général, un CFI supérieur à 0.90 est considéré comme indiquant un bon ajustement du modèle, tandis qu’un CFI supérieur à 0.95 est souvent interprété comme excellent.
Comme le CFI, le TLI compare le modèle testé à un modèle nul où il n’y a pas de relations entre les variables observées. Cependant, contrairement au CFI, le TLI pénalise la complexité du modèle; il ajuste la statistique d’ajustement en fonction du nombre de paramètres estimés, ce qui signifie qu’il prend en compte le degré de liberté. Cela peut rendre le TLI plus strict, surtout pour des modèles très complexes.
Le TLI varie également entre 0 et 1, avec des valeurs plus proches de 1 indiquant un meilleur ajustement. En général, un TLI supérieur à 0.90 est considéré comme indiquant un bon ajustement, tandis qu’un TLI supérieur à 0.95 est souvent interprété comme excellent.
Le RMSEA est un indice utilisé dans la modélisation par équations structurelles (SEM) pour évaluer la qualité de l’ajustement d’un modèle aux données observées. Cet indice mesure l’écart entre le modèle hypothétique et la réalité observée. Des valeurs plus faibles de RMSEA indiquent un meilleur ajustement. En général, un RMSEA inférieur à 0,05 est considéré comme un bon ajustement, tandis qu’un RMSEA entre 0,05 et 0,08 est jugé acceptable.
Le SRMR est un indice utilisé dans la modélisation par équations structurelles (SEM) pour évaluer la qualité de l’ajustement d’un modèle aux données observées. Cet indice mesure la différence moyenne entre les corrélations observées et les corrélations prédites par le modèle. Des valeurs plus faibles de SRMR indiquent un meilleur ajustement. En général, un SRMR inférieur à 0,08 est considéré comme un bon ajustement.
Pour obtenir spécifiquement ces indices, il faut utilier la syntaxe suivante avec un objet lavaan, c’est-à-dire la sortie des fonctions sem() ou cfa().
fitmeasures(object, fit.measures = c("chisq", "df", "pvalue",
"cfi", "tli", "RMSEA", "SRMR"))En tout, lavaan produit 46 indices statistiques différents. Ceux recommandés ici sont les mêmes que ceux rapportés par le logiciel Mplus (Caron, 2018). Il peut être intéressant de vérifier les autres options, surtout que certains pourront être spécifique à certains doomaines. Cela se fait simplement en laissant vide l’argument fit.measures qui par défaut est fit.measures = "all".
21.2.2 Les indices de modification
Il est rare que le modèle testé atteint les critères généraux d’ajustement du premier coup. Ainsi, il est possible d’améliorer le modèle en le peaufinant. La fonction modindices() suggère différents opérateurs à ajouter au modèle initial. Pour utiliser la fonction, il faut lui fournir un objet de classe lavaan (une sortie sem() ou cfa).
modindices(object, sort = TRUE)L’argument sort = TRUE permet d’avoir les arguments en ordre d’importances. La sortie peut devenir rapidement encombrante. Il est possible de raccourcir le fonction avec les arguments minimum.value, l’indice de modification minimale désiré, et maximum.number, le nombre d’opérateur suggéré maximale.
La fonction produit des résultats athéoriques qui ne font parfois aucun sens. Elle ne donne que des suggestions sur le plan statistique, jamais conceptuel ou théorique. C’est à l’utilisateur d’être judicieux dans ses choix. Par exemple, il est recommandé de d’abord envisager des covariances ~~, car celles-ci sont les moins contraignantes sur le plan théoriques. Les opérations =~, et ~ peuvent être envisagées par la suite si elles sont justifiables théoriquement.
Une dernière recommandation : il est préférable de tester séquentiellement les ajouts. Autrement dit, éviter d’ajouter plusieurs opérateurs simultanément et vérifier à chaque étape la pertinence des ajouts précédents.
21.2.3 Les résultats standarisés
La fonction standardizedSolution du package lavaan est utilisée pour extraire les solutions standardisées des modèles d’équations structurelles (SEM). Ces solutions fournissent des coefficients standardisés qui facilitent l’interprétation des relations entre les variables dans le modèle, en éliminant les effets des unités de mesure.
standardizedSolution(object)21.3 Analyse factorielle confirmatoire
Voici un exemple d’analyse factorielle exploratoire. La syntaxe suivante recrée le modèle présenté au chapitre Explorer. La matrice de corrélation se trouve dans le package Rnest (Caron, 2023) pour aller plus rapidement.
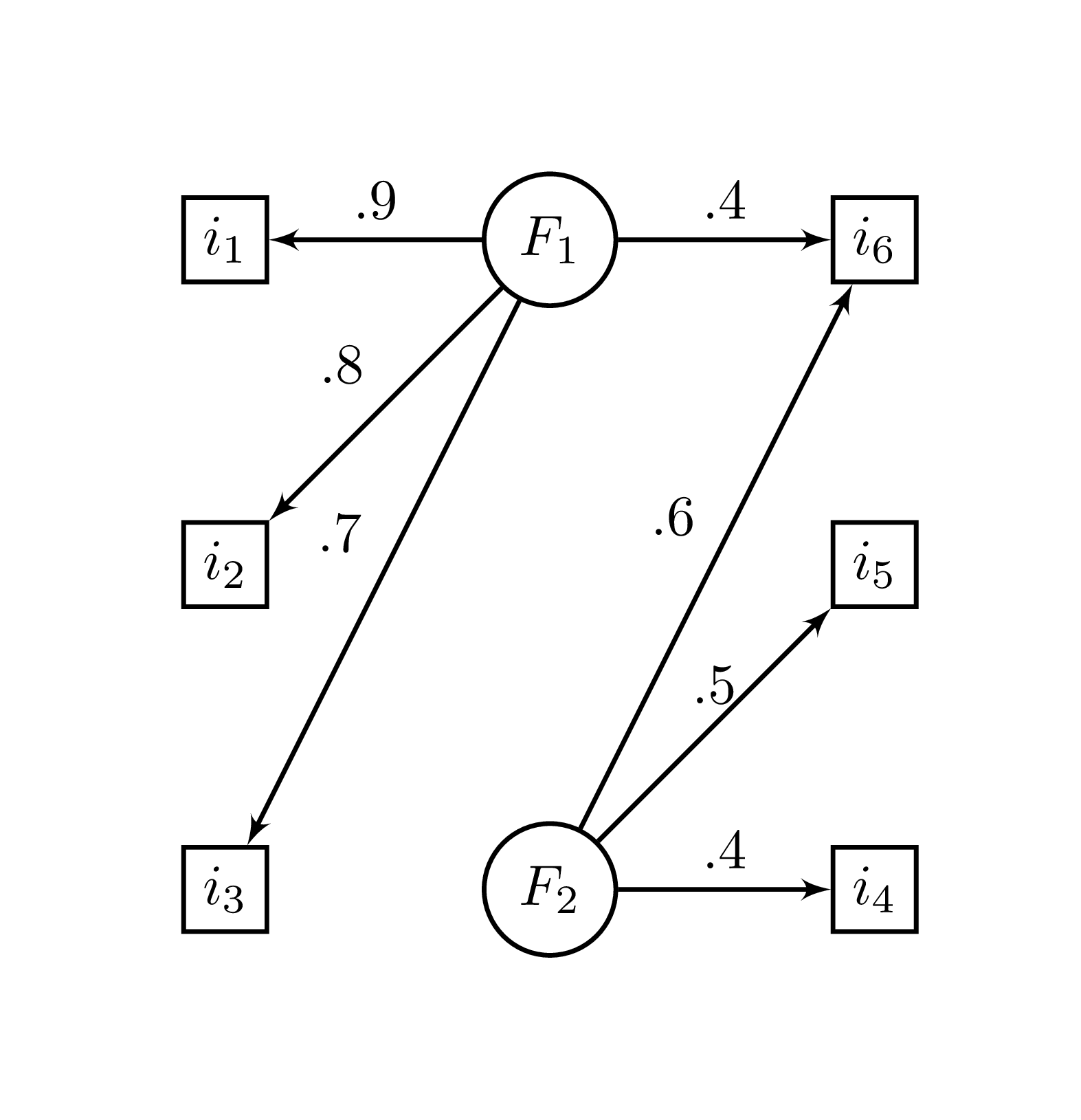
Figure 21.1: Structure factorielle de l’exemple
La Figure 21.1 (présentée auparavant à la Figure 19.1) montre la structure factorielle sous-jacente à la matrice de corrélation ex_mqr. La syntaxe crée un jeu de données basée sur cette matrice.
# Création de la matrice de recette de fabrication
R <- Rnest::ex_mqr
set.seed(32)
# Création du jeu de données
jd.cfa <- MASS::mvrnorm(n = 500,
mu = rep(0, ncol(R)),
Sigma = R)La première étape des modèles par équations structurelles est de définir le modèle. Dans la syntaxe, deux facteurs sont créés à partir des items qui devraient les composer. Ici, le lien F1 =~ i6 est intentionnellement omit. L’ajout de F1 ~~ 0*F2 qui fixe la covariance entre F1 et F2 à 0, ce qui facilitera la convergence de l’analyse dans ce cas spécifique.
model.cfa1 <- "
F1 =~ i1 + i2 + i3
F2 =~ i4 + i5 + i6
F1 ~~ 0*F2
"Une fois le modèle transcrit, il faut le rouler avec la fonction cfa() en incluant les données et le modèle
res.cfa1 <- cfa(model.cfa1, data = jd.cfa)
# sem() fonctionne également
# res.sem1 <- sem(model.cfa1, data = jd.cfa)À la place de F1 ~~ 0*F2, l’orthogonalité des facteurs aurait pu être demandé avec orthogonal = TRUE. Autrement, les facteurs sont obliques (libres d’être corrélés) par défaut.
res.cfa1 <- cfa(model.cfa1, sample.cov = cor(jd.cfa), sample.nobs = 60)Pour juger du modèle, les indices d’ajustement sont extraits.
fitmeasures(res.cfa1, c("chisq", "df", "pvalue",
"cfi", "tli", "RMSEA", "SRMR"))
> chisq df pvalue cfi tli rmsea srmr
> 76.571 9.000 0.000 0.909 0.848 0.123 0.117Les indices pourraient être légèrement amélioré ici. Notamment, le tli est trop faible (en bas de .90), le rmsea et le srmr sont trop élevés (au dessus de .08) et le chisq est significatif à \(p<.001\). La modification d’indice est demandée pour vérifier les possibles amélioreration du modèle.
modindices(res.cfa1, sort = TRUE)
> lhs op rhs mi epc sepc.lv sepc.all sepc.nox
> 18 F1 =~ i6 62.727 0.405 0.352 0.353 0.353
> 7 F1 ~~ F2 27.312 0.136 0.339 0.339 0.339
> 26 i1 ~~ i6 11.008 0.087 0.087 0.260 0.260
> 19 F2 =~ i1 8.583 0.243 0.112 0.117 0.117
> 30 i2 ~~ i6 5.293 0.064 0.064 0.127 0.127
> 24 i1 ~~ i4 2.594 -0.043 -0.043 -0.120 -0.120
> 29 i2 ~~ i5 2.470 -0.045 -0.045 -0.086 -0.086
> 25 i1 ~~ i5 2.464 0.042 0.042 0.122 0.122
> 16 F1 =~ i4 1.948 -0.072 -0.063 -0.063 -0.063
> 32 i3 ~~ i5 1.080 -0.034 -0.034 -0.056 -0.056
> 20 F2 =~ i2 0.762 0.077 0.035 0.038 0.038
> 31 i3 ~~ i4 0.318 0.018 0.018 0.029 0.029
> 33 i3 ~~ i6 0.258 0.016 0.016 0.027 0.027
> 17 F1 =~ i5 0.196 -0.023 -0.020 -0.020 -0.020
> 28 i2 ~~ i4 0.147 0.011 0.011 0.020 0.020
> 21 F2 =~ i3 0.002 -0.005 -0.002 -0.002 -0.002Les résultats montrent en ordre décroissant, des modifications à apporter au modèle qui pourraient l’améliorer. Les colonnes lhs, op et rhs représente l’ajout à fait et mi l’indice de modification. Plus ce dernier est élevé, plus il devrait améliorer le modèle une fois ajouter. En général, il faut privilégié les opérateurs comme ~~ soit une covariance entre deux variables, car elles sont moins contraignantes théoriquement. Les opérations =~, et ~ peuvent être envisagées si elles sont théoriquement soutenues.
Tel qu’attendu, les indices de modifications suggèrent ici d’ajouter le lien F1 =~ i6 dans le modèle. Normalement, cela serait à éviter à cause des implications théoriques, mais comme la structure de la population est connue, il s’agit bel et bien de la bonne solution.
Il faut par la suite réaliser de nouveau l’analyse pour tester le nouveau modèle.
model.cfa2 <- "
F1 =~ i1 + i2 + i3 + i6
F2 =~ i4 + i5 + i6"
res.cfa2 <- cfa(model.cfa2, data = jd.cfa)Les indices d’ajustement sont inspectés de nouveaux.
fitmeasures(res.cfa2, c("chisq", "df", "pvalue",
"cfi", "tli", "RMSEA", "SRMR"))
> chisq df pvalue cfi tli rmsea srmr
> 6.305 7.000 0.505 1.000 1.002 0.000 0.014Ils sont tous excellents et respectent les recommandations.
Grâce au package lavaanExtra (Thériault, 2023) il est possible de produire rapidement une figure des résultats finaux. Il faut absolument avoir installer les packages rsvg et DiagrammeRsvg pour obtenir la figure.
lavaanExtra::cfa_fit_plot(model.cfa2, data = jd.cfa)
Figure 21.2: Représentation graphiques de la structure factorielle finale
Enfin, les paramètres pourront être extraits si l’utilisateur désire les observés.
# Estimés non standardisés
parameterestimates(res.cfa2)# Estimés standardisés
standardizedSolution(res.cfa2)
> lhs op rhs est.std se z pvalue ci.lower ci.upper
> 1 F1 =~ i1 0.903 0.022 41.06 0.000 0.860 0.946
> 2 F1 =~ i2 0.754 0.026 29.03 0.000 0.703 0.805
> 3 F1 =~ i3 0.690 0.029 24.20 0.000 0.634 0.746
> 4 F1 =~ i6 0.318 0.048 6.66 0.000 0.225 0.412
> 5 F2 =~ i4 0.474 0.058 8.13 0.000 0.360 0.588
> 6 F2 =~ i5 0.552 0.063 8.80 0.000 0.429 0.675
> 7 F2 =~ i6 0.528 0.062 8.51 0.000 0.407 0.650
> 8 i1 ~~ i1 0.184 0.040 4.63 0.000 0.106 0.262
> 9 i2 ~~ i2 0.432 0.039 11.02 0.000 0.355 0.508
> 10 i3 ~~ i3 0.524 0.039 13.29 0.000 0.446 0.601
> 11 i6 ~~ i6 0.578 0.066 8.79 0.000 0.449 0.707
> 12 i4 ~~ i4 0.776 0.055 14.06 0.000 0.668 0.884
> 13 i5 ~~ i5 0.695 0.069 10.03 0.000 0.559 0.831
> 14 F1 ~~ F1 1.000 0.000 NA NA 1.000 1.000
> 15 F2 ~~ F2 1.000 0.000 NA NA 1.000 1.000
> 16 F1 ~~ F2 0.122 0.074 1.66 0.097 -0.022 0.26621.4 Analyse acheminatoire
Comme second exemple basé sur les analyses acheminatoires, il s’agit d’un modèle tiré de Lemardelet & Caron (2022) dont le jeu de données est disponible du package pathanalysis (Caron, 2021). Le modèle est une médiation sérielle avec deux médiateurs. La Figure 21.3 présente le modèle.
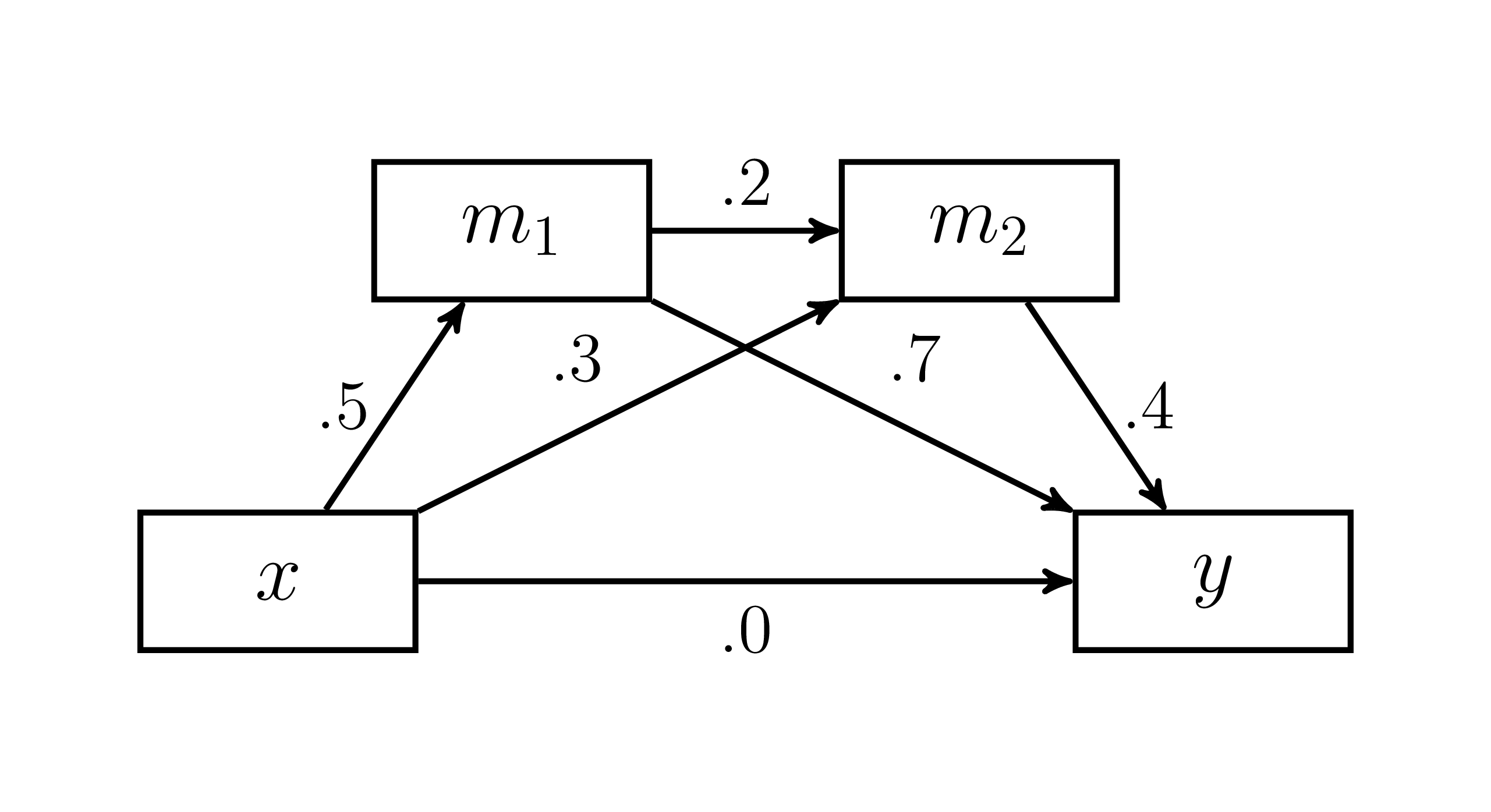
Figure 21.3: Modèle de médiation de Lemardelet et Caron (2022(
Le jeu de données se trouve dans le packages pathanalysis sous le libellé medEx.
jd.med <- pathanalysis::medEX
model.med1 <- "
m1 ~ x
m2 ~ x + m1
y ~ m2 + m1 + x" Une première transcription du modèle illustré à la Figure 21.3 est la syntaxe ci-dessus. Tous les liens sont bien inscrits, ce qui permet seulement d’estimer les liens directs (voir Médier).
Dans le cas de la médiation, il est désirable de calculer l’effet indirect en nommant les paramètres et définissant le ou les effets indirects. Comme le souligne Lemardelet & Caron (2022), un modèle à deux médiateurs sérielles se décompose en cinq effets indirects spécifiques, qui sont exprimés dans la syntaxe ci-dessous.
model.med2 <- "
m1 ~ a1*x
m2 ~ a2*x + b2*m1
y ~ c2*m2 + c1*m1 + d*x
ind_x_m1_m2_y := a1 * b2 * c2
ind_x_m1_y := a1 * c1
ind_x_m2_y := a2 * c2
ind_x_m1_m2 := a1 * b2
ind_m1_m2_y := b2 * c2
total_ind := a1 * c1 + a1 *b2 * c2 + a2 * c2
total := total_ind + d"Bien que ce modèle décrit cinq effets indirects, seulement trois sont importants pour l’analyse des médiateurs, ceux qui débutent de la variable indépendante jusqu’à la dernière variable dépendante du modèle. L’effet indirect total correspond à la somme de ces trois liens (dans cet exemple). Les deux autres, les effets indirects simple entre les médiateurs pourraient ou non être d’intérêt pour l’utilisateur. L’effet direct total correspond au lien entre la variable indépendante et dépendante en l’absence des médiateurs.
La syntaxe ci-dessus extrait en plus l’effet indirect totale, la somme de tous les effets indirects débutant par la variable indépendante jusqu’à la dernière variable dépendante du modèle et l’effet total.
res.lav.med2 <- sem(model.med2, data = jd.med)Voici la sortie.
# parameterestimates(res.lav.med2)
standardizedSolution(res.lav.med2)Pour désencombrer la sortie de la fonction (pour mieux présenter pour ce chapitre), voici la sortie avec un peu moins de colonnes.
standardizedSolution(res.lav.med2)[,-c(1:3,7,9:10)]
> label est.std se pvalue
> 1 a1 0.492 0.034 0.000
> 2 a2 0.181 0.044 0.000
> 3 b2 0.464 0.041 0.000
> 4 c2 0.666 0.031 0.000
> 5 c1 -0.016 0.038 0.667
> 6 d 0.252 0.034 0.000
> 7 0.758 0.034 0.000
> 8 0.669 0.036 0.000
> 9 0.371 0.027 0.000
> 10 1.000 0.000 NA
> 11 ind_x_m1_m2_y 0.152 0.020 0.000
> 12 ind_x_m1_y -0.008 0.018 0.667
> 13 ind_x_m2_y 0.121 0.030 0.000
> 14 ind_x_m1_m2 0.228 0.026 0.000
> 15 ind_m1_m2_y 0.309 0.033 0.000
> 16 total_ind 0.265 0.030 0.000
> 17 total 0.517 0.033 0.000Ici, le modèle est saturé, mais il est tout de même possible d’obtenir les indices d’ajustement. Si le modèle n’était pas saturé (s’il y avait des paramètres libres), il faudrait les vérifier comme l’exemple précédent.
fitmeasures(res.lav.med2, c("chisq", "df", "pvalue",
"cfi", "tli", "RMSEA", "SRMR"))
> chisq df pvalue cfi tli rmsea srmr
> 0 0 NA 1 1 0 0La Figure 21.4 obtenue par lavaanExtra montre le modèle final.
lavaanExtra::nice_lavaanPlot(res.lav.med2)Figure 21.4: Représentation graphiques du modèle acheminatoire