12 Simuler

Dans plusieurs contextes statistiques, les informations cruciales pour réaliser une analyse statistique ou tirer des résultats spécifiques ne sont pas connues (par exemple, le chapitre Analyser présente des analyses soutenues par des théorèmes). Pire, parfois certains postulats sont violés rendant les démarches usuelles caduques. Dans certains contextes, une analyse formelle pourrait s’avérer fort complexe, voire irrésolvable, alors qu’une analyse plus empirique usant des techniques de rééchantillonnage résoudra ces problèmes simplement et immédiatement.

Jusqu’à présent, les situations des analyses statistiques étaient connues. Maintenant, ce sont les techniques nécessitant moins de prérequis statistiques, comme le bootstrap et les simulations Monte-Carlo qui seront présentés.

12.1 Les simulations Monte-Carlo

Les simulations Monte-Carlo sont une famille de méthode algorithmique qui permet de calculer une valeur numérique en utilisant des procédés aléatoires. Le nom provient du prestigieux casino de Monte-Carlo à Monaco sur la Côte d’Azur, où des jeux de hasard se jouent constamment, et ayant ainsi une connotation très forte avec le hasard et les nombres aléatoires.

Une simulation de Monte-Carlo prédit une étendue de résultats possibles à partir d’un ensemble de valeurs d’entrée fixes et en tenant compte de l’incertitude inhérente de certaines variables. En d’autres termes, une simulation de Monte-Carlo produit les résultats possibles (sorties) d’un modèle à partir des entrées fixes et d’autres entrées variables. Ces sorties sont calculées encore et encore (des milliers de fois, parfois plus), en utilisant à chaque fois un ensemble différent de nombres aléatoires, générant des sorties probables, mais différentes à chaque fois. Les estimations (et leur tendance) obtenues peuvent alors être interprétées.

Les simulations Monte-Carlo sont particulièrement utiles, car elles permettent, en mathématiques, de calculer des intégrales très complexes; en physique, d’estimer la forme d’un signal ou la sensibilité; en finance, de recréer des conditions permettant de prévoir le marché; et en psychologie, de simuler des processus comportementaux ou cognitifs.

Les simulations Monte-Carlo possèdent trois caractéristiques :

Construire un modèle ayant des variables indépendantes (entrées) et dépendantes (sorties);
Spécifier les caractéristiques aléatoires des variables indépendantes et définir des valeurs crédibles;
Rouler les simulations de façon répétitive jusqu’à ce que suffisamment d’itérations soient produites et que les résultats convergent vers une solution.

Maintenant, ces étapes sont mises en contexte avec un problème.

12.1.1 Le problème de Monty-Hall

Rien de mieux pour confronter le sens commun que d’être confronté à un problème contre-intuitif. Les simulations Monte-Carlo nous permettront de vérifier les résultats de façon empirique, parallèlement à ce qu’une analyse formelle fournit.

Le problème de Monty Hall (attribuables à Selvin, 1975) présente un joueur devant un présentateur (Monty Hall). Trois portes sont offertes au choix du joueur. Derrière l’une d’entre elles se retrouve un magnifique prix : une voiture électrique de luxe. Derrière chacune des deux autres portes se retrouvent un prix citron : une chèvre chacune. Le joueur ne sait pas ce qu’il y derrière les portes. Le joueur peut alors choisir une porte. Évidemment, à ce moment le joueur à une chance sur trois de choisir la voiture.

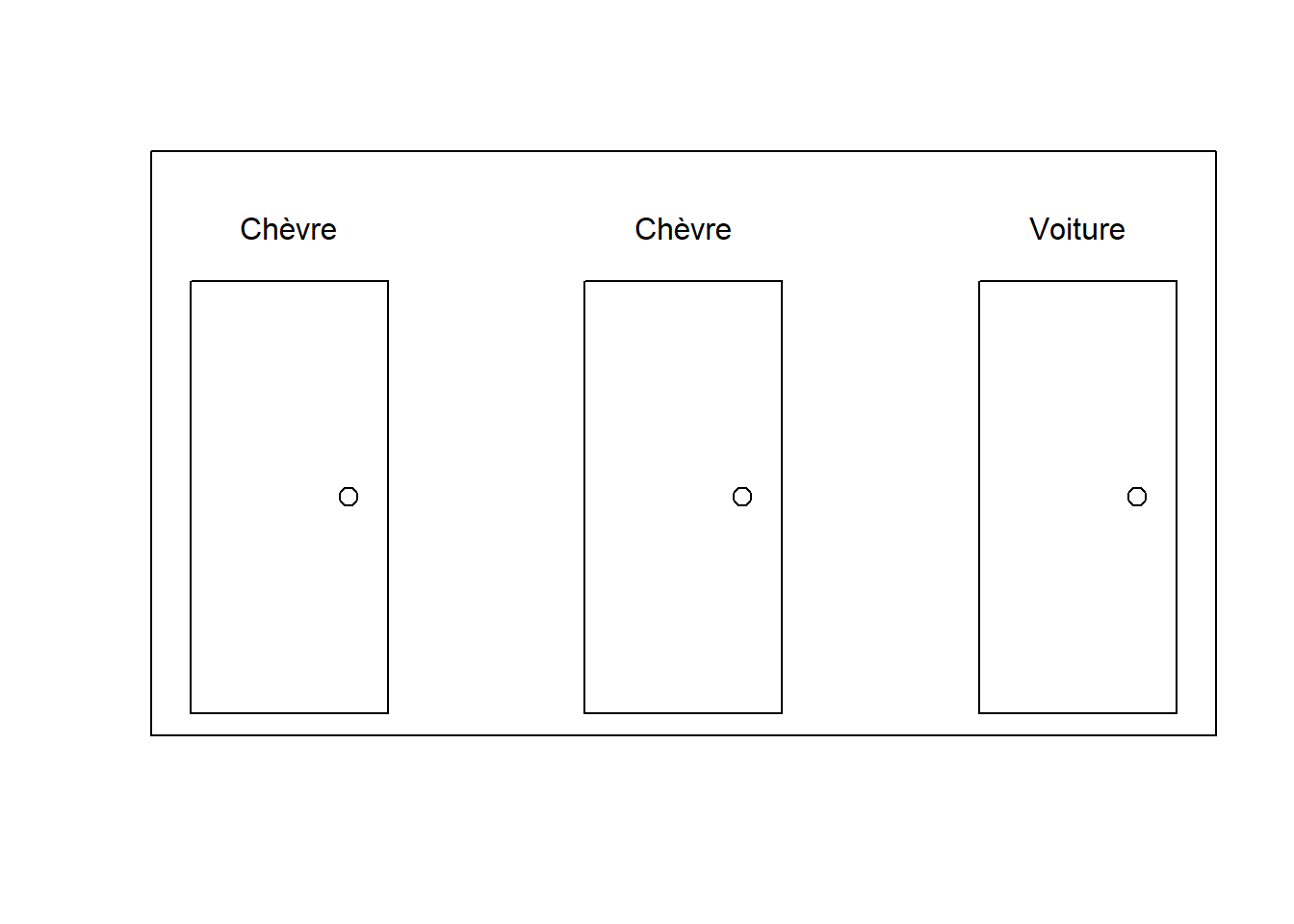
Figure 12.1: Illustration du problème de Monty Hall

Par la suite, le présentateur, qui connaît le contenu derrière les portes, ouvre une porte qui (a) ne cache pas la voiture et (b) que le participant n’a pas choisie. Le joueur peut alors choisir (a) de conserver la porte choisie ou (b) de changer de porte. Quelle option, s’il y en a une, assurera la meilleure probabilité de choisir la voiture? Rester ou changer? Par exemple, suivant l’illustration de la Figure 12.1, le joueur choisit la porte 1, alors le présentateur doit ouvrir la porte 2 (non choisie et ne contient pas la voiture). Le joueur doit-il changer son choix? Ici, la réponse est évidente, car la réponse est connue. Qu’en est-il alors si le joueur a choisi la porte 3 et le présentateur ouvre l’une des deux autres porte? Le joueur doit-il changer ou rester? La question sous-jacente est qu’elles sont les probabilités de rester et de changer respectivement. Sont-elles différentes?

Comme le résultat n’est pas des plus intuitif (et sans divulgâcher le résultat), une petite simulation s’impose (ou une analyse formelle pour les lecteurs enclins mathématiquement). La situation sera recréée un millier de fois pour vérifier l’option (rester ou changer) qui maximise de gagner la voiture.

En se référant aux trois points caractérisant une simulation Monte-Carlo susmentionné :

Le problème de Monty Hall tel qu’imminemment décrit.
Les variables indépendantes sont

le tirage aléatoire du contenu derrière les portes (distribution uniforme, chaque porte à la même probabilité d’avoir un prix ou non);
le choix du joueur (distribution uniforme, pourrait être différent), et;
la porte ouverte par le présentateur,
l’action de rester ou de changer (les deux options sont étudiées).

Il y a une variable dépendante :

le succès (gagner le prix) ou l’échec (ne pas gagner le prix).

La simulation est reprise 1000 fois.

Les étapes de la simulation se déroulent ainsi.

L’attribution des portes (une gagnante et deux perdantes) est faite aléatoirement¹¹.
Le joueur fait son premier choix.

Plusieurs modèles peuvent être utilisés, comme systématiquement choisir la même porte, ce qui simplifie la situation et ne change pas les probabilités, car le contenu derrière les portes est aléatoire. Pour rester vrai à la situation, le joueur fait un choix aléatoire.

Le comportement du présentateur s’enclenche, il doit “ouvrir” une porte non choisie et qui ne contient pas le prix.
Les deux stratégies sont simulées, rester ou changer.
La simulation enregistre s’il y a eu gain ou non et l’additionne au total de chacun.
La simulation est reprise un nombre important de fois, ici, 1000 suffit, mais des situations compliquées peuvent demander beaucoup plus d’itérations.

# Simulation du problème de Monty Hall
# Valeurs possibles des portes
portes <- c("Chèvre", "Chèvre", "Voiture")
# Nombre de répétitions
nreps <- 1000
# Pour la reproductibilité
set.seed(7896)

# Valeur initiale des gains
gain.rester <- 0
gain.changer <- 0

# Boucle pour répéter `nreps` fois le scénario
for(i in 1:nreps){
  
  # Arrangement initial des portes
  tirage <- sample(portes)
  
  # Trouver le prix
  prix <- which(tirage %in% "Voiture")
  
  # Choix aléatoire
  choix1 <- sample(length(portes), size = 1)
  
  # Sélectionner la porte avec la chèvre (pas un prix) et
  # qui n'est pas celle choisie (choix1)
  option <- c(choix1, prix)
  
  if(choix1 != prix){
    
    # Si une porte valide
    monty <- c(1:3)[-option]
    
  }else{
    
    # Si deux portes valides, en choisir une aléatoirement.
    monty <- sample(c(1:3)[-option], size = 1)
    
  }
  
  # Décision : Reste à choix1
  choix.rester <- choix1
  
  # Décision : Changer de choix changer
  # Changer = ne pas prendre la porte initial, ni la porte ouverte
  choix.changer <- c(1:3)[-c(choix1, monty)]
  
  # Enregistrement des gains
  gain.rester  <- gain.rester  + 
                   (tirage[choix.rester]  == "Voiture")
  gain.changer <- gain.changer + 
                   (tirage[choix.changer] == "Voiture")
}

cbind(gain.rester, gain.changer) / nreps
>      gain.rester gain.changer
> [1,]       0.316        0.684

Une petite digression avant de poursuivre. Il faut être naïf pour croire que le code fonctionne tel que prévu. À cause d’un inconvénient de la fonction sample(), une approche conditionnelle doit être utilisée. En fait, la fonction échantillonne les éléments de x (premier argument) jusqu’à obtenir size objets. Par contre, si une seule valeur est donnée à x et qu’elle est numérique, alors la fonction utilise les éléments de 1:x pour rééchantillonner au lieu de retourner x. Ainsi, si le choix et le prix (porte 2) sont derrière des portes différentes (porte 1 et 2, par exemple), alors une seule valeur est retournée (3), et sample() utilise 1:3 au lieu de 3. Ces particularités expliquent et justifient l’utilisation d’une formule conditionnelle. En programmation, il faut toujours s’assurer que les fonctions s’accordent avec les attentes. Ce cas est documenté et délibéré (voir ?sample), mais surprend.

Quelles sont les résultats de cette simulation? Le fait de rester sur le premier choix devrait obtenir 33% de chance de réussir, comme le joueur a initialement une chance sur trois d’avoir la bonne réponse. Qu’en est-il pour changer? Est-ce qu’ouvrir une porte chèvre modifie les probabilités? Les résultats de la simulation montre que rester gagne 31.6% et que changer gagne 68.4%. À long terme, il est plus avantageux de changer.

Une explication simple est de dénombrer les possibilités. Dans le cas où le joueur ne change pas d’idée, il a une chance sur trois, soit : choisir la chèvre 1, et garder la chèvre 1; choisir la chèvre 2, et garder la chèvre 2; et choisir la voiture, et garder la voiture. Si le joueur change d’idée après l’ouverture des portes, les chances sont maintenant de deux sur trois, soit choisir la chèvre 1, changer pour le prix; choisir la chèvre 2 et changer pour le prix; ou choisir le prix et changer pour une chèvre.

Une autre façon de rendre se problème plus intuitif est de considérer le problème avec 100 portes au lieu de 3. Le présentateur ouvre les 98 portes qui ne sont pas un prix. Si le joueur choisit une porte et garde, il a effectivement 1% de chance de remporter le prix. Par contre, s’il choisit une porte et que le présentateur lui ouvre toutes les autres portes chèvres, le joueur gagne à tout les coups s’il change, sauf s’il a choisi le prix au premier coup. C’est comme si le participant ouvrait les 99 portent, sauf celle qu’il a choisit au début.

Avec quelques modifications de la syntaxe précédente, le code suivant illustre le cas à 100 portes. À noter que l’usage du conditionnelle n’est plus nécessaire au bon fonctionnement de sample(), car il y a maintenant plus de trois portes.

# Simulation du problème de Monty Hall
portes <- c("Voiture", rep("Chèvre", 99))
n <- length(portes)
nreps <- 1000
set.seed(7896)

# Valeur initial des gains
gain.rester <- 0
gain.changer <- 0

for(i in 1:nreps){
  # Arrangement initial des portes
  tirage <- sample(portes)
  
  # Trouver le prix
  prix <- which(tirage %in% "Voiture")
  
  # Choix aléatoire
  choix1 <- sample(n, size = 1)
  
  # Sélectionner la porte avec la chèvre (pas un prix) et
  # qui n'est pas celle choisie (choix1)
  option <- c(choix1, prix)
  
  # Les autres portes
  monty <- sample(c(1:n)[-option], size = n - 2)
  
  # Décision : Reste à choix1
  choix.rester <- choix1
  
  # Décision : Changer de choix changer
  # Changer = ne pas prendre la porte initial, ni la porte ouverte
  choix.changer <- c(1:n)[-c(choix1, monty)]
  
  # Enregistrement des gains
  gain.rester <- gain.rester + 
                  (tirage[choix.rester] == "Voiture")
  gain.changer <- gain.changer + 
                  (tirage[choix.changer] == "Voiture")
}

cbind(gain.rester,gain.changer)  / nreps
>      gain.rester gain.changer
> [1,]       0.009        0.991

La simulation montre que rester gagne 0.9% et que changer gagne 99.1%.

Des situations fort plus compliquées peuvent être apportées en simulations Monte-Carlo. Le jeu de Black Jack en est un exemple, bien qu’il soit déjà résolu pour des résultats optimaux (Millman, 1983). Peu importe la situation à simuler, il suffit d’avoir la patience de la programmer pour confirmer les résultats analytiques.

Sur le plan pratique pour l’expérimentateur, les simulations Monte-Carlo peuvent être utiles pour calculer des tailles d’échantillons pour des modèles complexes, comme des modèles par équations structurelles compliquées, multiniveaux ou de classes latentes. Il peut être utile également pour imiter des processus cognitifs ou comportementaux. Toutefois, une sous-famille est d’une importance significative pour l’expérimentateur, celle qui sera abordée maintenant, le bootstrap.

12.2 Le bootstrap

Le bootstrap (dont il n’y a pas d’excellente traduction en français) est une des techniques de rééchantillonnage astucieuses permettant des inférences statistiques (Efron & Tibshriani, 1979). Il fait partie de la famille des simulations Monte-Carlo, car il se base sur la réitération multiple d’une statistique à partir d’un jeu de données. Sans entrer dans les détails, il existe plusieurs types de techniques de bootstrap, qui font elles-mêmes parties d’une plus grande famille, les simulations stochastiques. Y est inclus les simulations de Monte-Carlo (dont le bootstrap fait parti) et les méthodes numériques bayésiennes.

Cet ouvrage insiste sur le bootstrap non paramétrique, impliquant que les distributions sous-jacentes aux échantillons ne soient pas spécifiées, bien qu’il existe du bootstrap paramétrique. Ce premier type de bootstrap est certainement la plus utile pour l’expérimentateur.

Dans le bootstrap, l’échantillon initial est considéré comme une pseudopopulation. Il ne nécessite pas d’autre information que celle fournie par l’échantillon. Il permet d’obtenir une distribution d’échantillonnage et tous ses bénéfices. Alors que dans les chapitres Inférer et Analyser, il faut préciser et connaître quelle distribution d’échantillonnage correspond à quelle statistique (p. ex., le score-\(z\) d’une unité à la distribution normale; la moyenne d’un échantillon à la distribution \(t\) si la variance est inconnue), aucune de ces connaissances n’est nécessaire. L’étendue d’application du bootstrap est immense, surtout pour les concepts statistiques qui offriront plus de défis, ce qui sera vu dans des chapitres ultérieurs.

Comme abordé dans le chapitre Inférer, la distribution d’échantillonnage permet :

d’estimer l’indice désiré;
d’estimer son erreur standard;
d’estimer ses intervalles de confiance;
de réaliser un test d’hypothèse;

tout cela en ignorant les distributions et postulats sous-jacents qui empêchent ou limitent leurs usages. Le bootstrap n’a que deux hypothèses fondamentales : l’échantillon reflète la population et chaque unité est indépendante et identiquement distribuée. Autrement dit, chaque unité provienne bel et bien d’une même boîte (population, voir Inférer) et le tirage d’une unité n’influence pas celle d’une autre.

Le fondement du bootstrap repose sur les étapes suivantes :

Sélectionner avec remise les unités d’un échantillon;
Calculer et enregistrer l’indice statistique désiré auprès de ce nouvel échantillon;
Réitérer les deux premières étapes un nombre élevé de fois.

Ce processus hautement facilité par l’excellente performance des ordinateurs d’aujourd’hui, se réalise très facilement et rapidement. L’exemple suivant se base sur le rééchantillonnage (1000 fois) de la moyenne à partir d’une variable aléatoire tirée d’une distribution uniforme avec un minimum de 5 et d’une maximum de 15.

set.seed(158)
# Nombre d'unités
n <- 30

# Le nombre de rééchantillonnage
nreps <- 10000

# Création de la variable
X <- runif(n = n, min = 5, max = 15)

# Création d'une variable vide pour l'enregistrement
moyenne.X <- numeric()

# L'utilisation d'une boucle permet de réitérer les étapes
for (i in 1:nreps){
  # Rééchantillonnage avec remise
  id <- sample(n, replace = TRUE)
  
  # Nouvel échantillon
  nouveau.X <- X[id]
  
  # Calculer et enregistrer la moyenne
  moyenne.X[i] <- mean(nouveau.X)
}

La fonction sample(, replace = TRUE) rééchantillonne avec remplacement les identifiants des unités. Par simplicité, il est possible d’éliminer la ligne nouveau.X = X[id] en utilisant mean(X[id]) ou plus simplement mean(sample(X, replace = TRUE)). Cette utilisation se limite seulement au cas d’un vecteur de données. S’il s’agit d’un jeu de données avec plus d’une variable, alors mean(X[id, ]) est utilisée. Noter l’usage de la , entre crochets. De cette façon, toutes les variables des unités identifiées par id sont extraites (voir Référer à une variable dans un jeu de données).

À partir des informations obtenues, des inférences statistiques sont possibles. Toutes les estimations sont présentées comme un histogramme tel que l’illustre la Figure 12.2. Le code se retrouve ci-dessous. Quelques formules pour améliorer la présentation se retrouvent dans la syntaxe. L’utilisation simple de hist() pourra convenir.

hist(moyenne.X,              # Données
     ylab = " Frequence",    # Changer l'axe y
     main = "",              # Retirer le titre
     breaks = 50,            # Nombre de colonnes
     xlim = c(7,13)          # Définir l'étendu de l'axe x
)

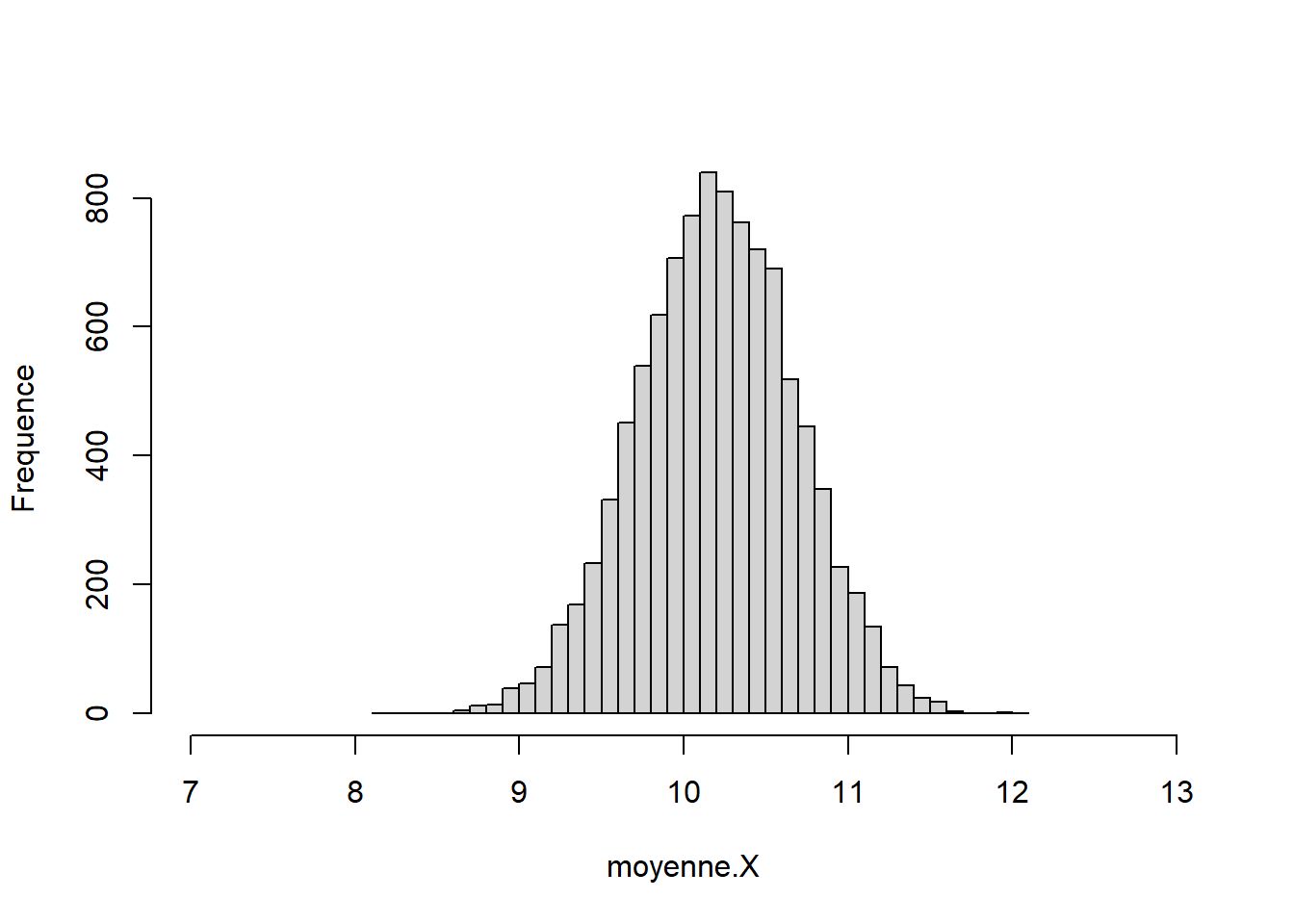
Figure 12.2: Historgamme des estimations des échantillons

La distribution de la Figure 12.2 se désigne comme la distribution d’échantillionnage, comme c’est le cas dans le chapitre sur les inférences Inférer. Elle agit comme distribution de la population de l’indice. Elle permet d’avoir une estimation plus robuste de l’erreur standard, qui se trouve à être l’écart type des indices rééchantillonnés. Elle est également utilisée pour construire des intervalles de confiance et permet ainsi de faire des tests d’hypothèse comme : l’intervalle de confiance à \((1-\alpha) \times 100\) % contient-elle la valeur 0? Comme il est fait avec une hypothèse nulle traditionnelle.

Le cas illustré est trivial au sens où, par le théorème central limite, la distribution des moyennes est déjà connue. Si l’exemple était plutôt sur la médiane, il faudrait obligatoirement procéder par bootstrap pour calculer son erreur type et ses intervalles de confiance, car aucune formule exacte ne permet sa dérivation (il existe bien des approximations cela dit). Le bootstrap est alors des plus appropriés pour calculer l’erreur type et en tirer des intervalles de confiances, voire même en faire des tests d’hypothèses. Plusieurs statistiques auront recours au bootstrap pour dériver ces informations, la plus utilisée étant le coefficient de détermination (voir le chapitre sur la régression) ou la médiation pour tester les effets indirects.

À partir des informations obtenues auprès du rééchantillonnage, il est possible d’obtenir les éléments désirés. Comme le cas est trivial, les indices statistiques seront très similaires. Cela confirmera au lecteur qu’aucun principe ésotérique ne s’est déroulé devant ses yeux en plus de confirmer que les statistiques attendues se produisent effectivement.

# Voici la moyenne et l'erreur standard originales
mean(X) ; sd(X)/sqrt(n)
> [1] 10.2
> [1] 0.485

# La moyenne et l'erreur standard à partir des rééchantillons
mean(moyenne.X)  ; sd(moyenne.X)
> [1] 10.2
> [1] 0.481

La moyenne et l’erreur standard sont très près de la moyenne de l’échantillon et celle de la population (qui est de 10) et de l’erreur type attendue. Il est possible de créer des intervalles de confiances avec la fonction quantile qui prend en argument un vecteur de données et les probabilités désirées. Dans le cas de 95% pour une erreur de type I de 5%, soit \(\alpha=.05\), il s’agit de \(.05/2 = .025\) et \(1-.05/2= .975\), laissant au total 5% aux extrémités.

# Erreur de type I
alpha <- .05

# Valeurs critiques
crit <- c(alpha/2, (1-alpha/2))
tv <- qt(crit, df = n - 1)

# Intervalles basés sur les indices de l'échantillon
mean(X) + tv * sd(X)/sqrt(n)
> [1]  9.2 11.2

# Intervalles basés sur les indices du rééchantillonnage
mean(moyenne.X) + tv * sd(moyenne.X)
> [1]  9.22 11.18

# Intervalles sur le rééchantillonnage
quantile(moyenne.X, crit)
>  2.5% 97.5% 
>  9.26 11.13

Pour réaliser le test d’hypothèse nulle, il suffit de constater si l’intervalle de confiance contient ou non 0. Dans le cas où l’intervalle contient 0, le test n’est pas significatif; l’hypotèse nulle n’est pas rejetée; il est vraisemblable que l’absence d’effet soit vraie. S’il ne contient pas 0, l’hypothèse nulle est rejetée, le test est significatif et il est vraisemblable qu’il y ait un effet. Dans cet exemple, la moyenne est clairement différente de 0, car elle ne contient pas cette valeur.

12.2.1 Meilleures pratiques

R n’est pas particulièrement efficace pour réaliser des boucles. Il existe une famille de fonctions apply qui permet d’appliquer une fonction sur une série de vecteurs (comme une liste, un jeu de données ou une matrice). L’appel à l’aide ?apply donne beaucoup d’informations à ce sujet.

La fonction principale est apply(). Elle nécessite le jeu de données (X) sur lequel appliqué la fonction (FUN) et un argument (MARGIN) pour identifier la dimension selon laquelle il faut appliquer la fonction, comme MARGIN = 1 produit l’opération par lignes; MARGIN = 2 produit l’opération par colonnes.¹²

# Il faut un vecteur de données `vec`, un nombre de répétitions `nreps`
# et une fonction `theta` à calculer sur le vecteur
bootstrap <- function(vec, nreps, theta){
  btsp.vec <- matrix(sample(vec, nreps * length(vec), replace = TRUE),
                     nrow = nreps)
  btsp.res <- apply(X = btsp.vec, MARGIN = 1, FUN = theta)
  return(btsp.res)
}

# En utilisant les données de l'exemple précédent
btsp <- bootstrap(vec = X, nreps = nreps, theta = mean)

# Pour fin de comparaison :
# Voici la moyenne et l'erreur standard de ce bootstrap
mean(btsp)  ; sd(btsp)
> [1] 10.2
> [1] 0.484

# Voici la moyenne et l'erreur standard à partir du premier bootstrap
mean(moyenne.X)  ; sd(moyenne.X)
> [1] 10.2
> [1] 0.481

# Et voici la moyenne et l'erreur standard originales
mean(X) ; sd(X)/sqrt(n)
> [1] 10.2
> [1] 0.485

12.2.2 Les packages

Il existe plusieurs packages pour réaliser du bootstrap dans R. Il y a bootstrap (Tibshirani & Leisch, 2019) et boot (Canty & Ripley, 2021). Ajouter à cela que plusieurs fonctions R possèdent des options de bootstrap intégrées (qu’il faut commander dans les arguments). Plusieurs analyses statistiques recourant aux bootstraps sont déjà implantées. L’aperçu donné dans ce chapitre devrait convaincre le lecteur que, s’il a besoin de bootstrap, il est assez rudimentaire de l’implanter soi-même.

11 Analyser

Exercices