22 Classer
En plus d’essayer de regrouper des variables ensemble, il aussi possible d’essayer de regrouper les participants en groupes. Il s’agit de l’analyse de classes latentes (LCA) et l’analyse de profils latents (LPA). La LCA et la LPA se distinguent par le type de variables qu’elles considèrent, soit les variables continues (LPA) ou catégorielles (LCA). Ces techniques sont utiles lorsque l’expérimentateur souhaite réduire l’échantillon en sous-groupe afin de mieux comprendre les participants. Elles peuvent notamment permettre de décrire les profils de compétences et de difficultés parmi les enfants d’âge préscolaire, en identifiant ceux qui peuvent avoir besoin d’interventions éducatives spécifiques ou encore de décrire des groupes de résilience à la violence conjugale et de mieux orienter les interventions auprès des personnes ayant été victimes d’agressions sexuelles.
Ces analyses issues des modèles de mixture (mixture modelling) sont similaires aux techniques de regroupement (clustering), mais qui s’en distinguent car elles reposent sur un modèle explicite et prennent en compte le fait que les groupes identifiés sont incertains. Le modèle sous-jacent présenté à la Figure 22.1.
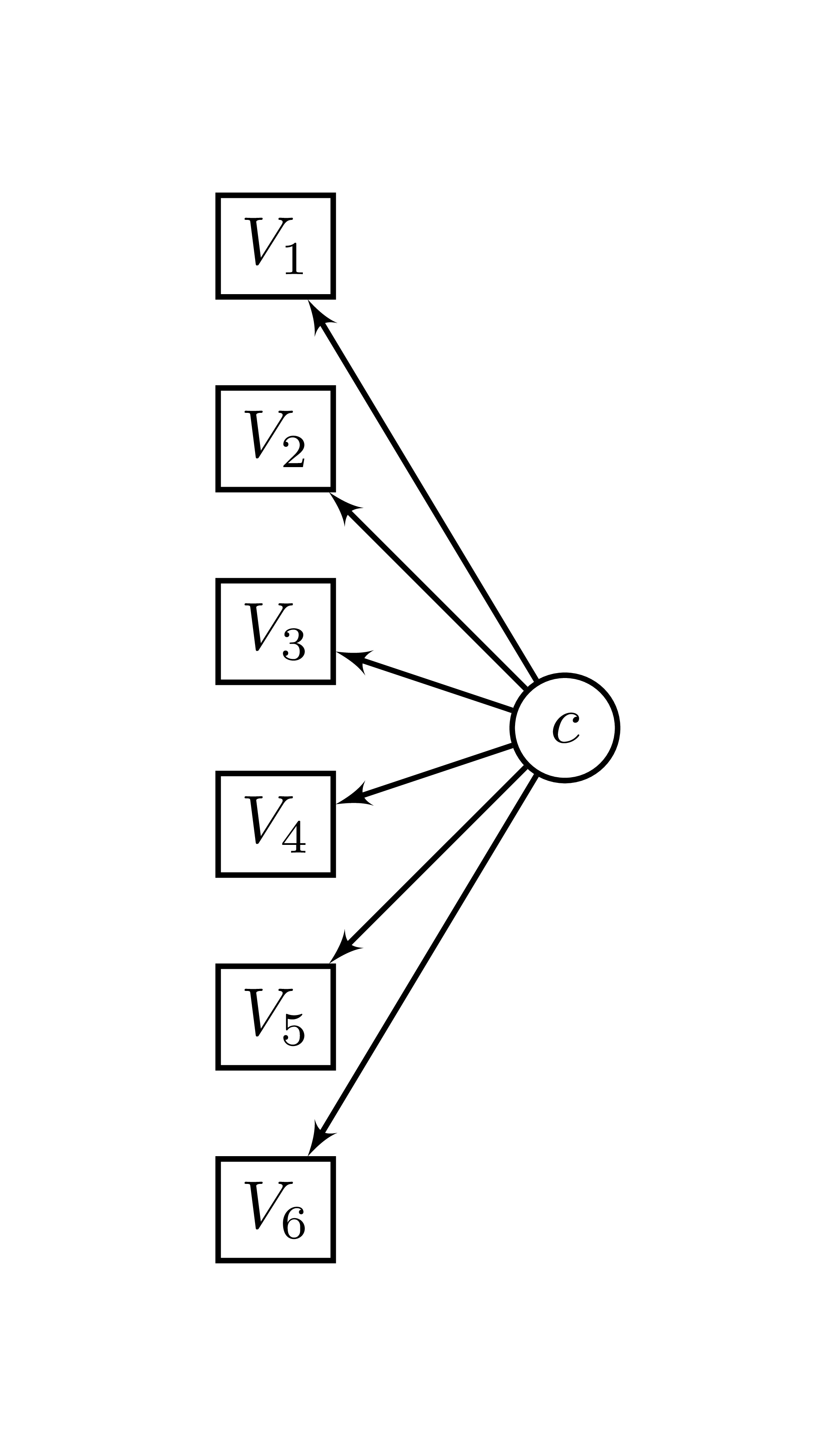
Figure 22.1: Modèle de classes latentes
La LCA et la LPA sont considérés comme plus robustes que les autres techniques, comme le k-mean, par exemple, par ce qu’elle repose sur un modèles théorique. Cela revient au détriment d’être plus intensif computationnellement, ce qui pourra soulever des problèmes à l’ocassion, surtout pour la LCA. Néanmoins, il demeure que les techniques de regroupement sont en quelque sorte un bricolage. Au final, c’est la solution qui fera le plus de sens sur le plan théorique qui sera retenu. Même si les statistiques suggéreront un certain nombre de classes, elles ne seront pas toujours en harmonie entre elles. C’est la simplicité et le pouvoir explicatif qui devra être l’ultime décideur.
22.1 Classes latentes
L’analyse de classes latentes (LCA) permet de partager et de distinguer des sous-groupes non observables (latents) d’individus sur la base de leurs réponses à un ensemble d’indicateurs observables (manifestes) ordinales. Elle fait ainsi partie de la famille des finite mixture modelling. Il s’agit d’une analyse exploratoire de la même façon que les [analyses factorielles exploratoires]. Elle se distingue d’analyse factorielle qui tente plutôt de regrouper les indicateurs en facteurs (ou groupe), alors que la LCA tente plutôt de regrouper les participants en groupe.
22.1.1 Installations
Il existe un package permettant de réaliser la LCA avec R, soit poLCA. Ce package bien qu’excellent pour réaliser la LCA demeure relativement incomplet et mérite quelques amélioration, ce pourquoi le package poLCAExtra est recommandé. Installer poLCAExtra installera du même coup le package poLCA.
# Version en développement sur GitHub
remotes::install_github(repo = "quantmeth/poLCAExtra")Une fois téléchargé, comme toujours, il faut appeler le package.
library(poLCAExtra)22.1.2 Déterminer le nombre de classes
La première étape est de déterminer le nombre de classes. Pour ce faire, on importe le jeu de données, ici ex1.poLCA, un jeu de données de poLCAEXtra. On spécifie ensuite le modèle dans une formule.
jd <- ex1.poLCA
f1 <- cbind(V1, V2, V3, V4, V5, V6) ~ 1Comme la Figure 22.1 montre, les items sont les variables dépendantes et comme la MANOVA, il faut indiquer ces variables à gauche de la formule en les liant avec cbind(), comme cbind(V1, V2, V3, V4, V5, V6). Le ~ délimite les variables dépendantes et dépendantes. L’utilisation de 1 indique la seule présence d’une constance, il serait possible d’ajouter des covariables pour contrôler des effets dans les variables dépendantes si l’utilisateur le jugeait nécessaire.
Ensuite, il faut rouler différentes valeurs de nombre de classes en incrément de 1.
LCA1 <- poLCA(f1, data = jd, nclass = 1, verbose = FALSE)
LCA2 <- poLCA(f1, data = jd, nclass = 2, verbose = FALSE)
LCA3 <- poLCA(f1, data = jd, nclass = 3, verbose = FALSE)
LCA4 <- poLCA(f1, data = jd, nclass = 4,
maxiter = 500, nrep = 4, verbose = FALSE)La fonction poLCA() prend en argument le jeu de donnée et la formule et le nombre de classes à rechercher. L’argument verbose = FALSE évite de polluer la console avec toutes les sorties de la fonction. Autrement, la fonction sort automatiquement la sortie même s’il y a assignation. Plus il y a de classes, plus le modèles est difficile à évaluer, c’est pourquoi à nclass = 4, les options maxiter et nrep sont ajoutées. Ces arguments augmenteront le nombre maximal d’itération et le nombre de répétions de départ, ce qui permettra d’assurer une meilleur estimation du modèle et aussi une meilleure stabilité. Bien que cela dépend de plusieurs facteurs, ces options deviennent obligatoire vers quatre classes. Et plus le modèle devient compliqué, plus ces valeurs devront augmentées. Il n’y a pas de critères définitifs pour ces valeurs, outre que plus, c’est mieux, mais plus long à calculer.
Pour les comparer, le package poLCAExtra permet la comparaison automatique des modèles avec la fonction anona().
anova(LCA1, LCA2, LCA3, LCA4)
> nclass df llike AIC BIC Classes.size Entropy
> 1 1 57 -2688 5388 5416 800 3.36
> 2 2 50 -2365 4757 4817 373|427 2.96
> 3 3 43 -2196 4432 4525 101|345|354 2.75
> 4 4 36 -2190 4435 4561 49|73|324|354 2.74
> Relative.Entropy LMR p
> 1
> 2 0.803 614.576 < .001
> 3 0.840 322.830 < .001
> 4 0.871 10.574 0.158Plus simplement, à l’aide de poLCAExtra, ces deux derniers chunks pourraient être remplacés par celui-ci qui tester toutes les classes de 1:4.
LCAE <- poLCA(f1, data = jd, nclass = 1:4,
maxiter = 500, nrep = 4)Dans cette sortie, plusieurs éléments pourront guidés la décision sur le nombre de classes. Généralement, on recourt au AIC, au BIC et l’entropie relative. Idéalement, il faudrait que le AIC et le BIC soit le plus faible possible avec des bonds importants entre chaque nombre de classes. Dans ce cas-ci ces deux indices commencent à augmenter à nclass = 4, ce qui laisse suggérer que trois classes est une bonne solution. Une autre recommandation est une entropie relative supérieure à .80. Il s’agit d’une allant de 0 à 1, le plus haut étant le meilleur. Ici, le modèle à quatre classes n’est pas soutenu. Il faudra jeter une regard à taille des classes afin d’éviter des classes trop petites ou disproportionnées. Cette taille varieront inévitablement d’une question de recherche à l’autre, mais il faut y porter attention. Ici, elle semble toute adéquate pour sauf l’option à deux classes. un dernier test souvent utilisé est le test de vraisemblance de Lo-Mendell-Rubin (LMR) qui fournit une valeur-p. Ce test suggère un nombre de classes jusqu’au premier modèle non-significatif (exclusivement). Ici, le LMR suggère trois classes, car la quatrième classes est non-significative au seuil de 5%. Ce test a tendance a être très libéral, il faut y recourir avec discernement.
22.1.3 Inspections
Une des hypothèses de la LCA est l’indépendance locale, soit qu’une fois les classes retirées, les variables observées sont indépendantes les unes des autres. Cela se traduit par l’absence de patterns entre les items non tenus compte par les classes. Pour vérifier cela, poLCAExtra ajoute la fonction poLCA.tech10() pour vérifier les patterns.
poLCA.tech10(LCA3)
>
> The 20 most frequent patterns
>
> pattern observed expected z chi llik.contribution
> 1 111111 200 201.26 -0.089 0.008 -2.504
> 23 122121 166 165.34 0.051 0.003 1.325
> 10 112121 48 47.67 0.048 0.002 0.662
> 17 121121 42 46.13 -0.608 0.369 -7.875
> 22 122111 39 37.76 0.202 0.041 2.520
> 3 111121 38 32.91 0.887 0.787 10.930
> 5 111211 32 30.69 0.236 0.056 2.669
> 50 222222 29 28.14 0.163 0.027 1.754
> 2 111112 25 27.20 -0.422 0.178 -4.219
> 8 112111 23 28.33 -1.001 1.001 -9.581
> 15 121111 22 18.61 0.787 0.619 7.373
> 26 122222 11 12.68 -0.473 0.224 -3.134
> 24 122122 10 10.90 -0.273 0.074 -1.724
> 27 211111 10 7.97 0.717 0.514 4.525
> 46 222122 9 8.92 0.026 0.001 0.159
> 25 122221 8 5.43 1.103 1.218 6.203
> 9 112112 7 2.99 2.320 5.382 11.914
> 42 221222 7 6.79 0.082 0.007 0.433
> 6 111212 6 4.25 0.848 0.720 4.135
> 14 112222 6 2.55 2.157 4.654 10.254
> p check
> 1 0.465
> 23 0.480
> 10 0.481
> 17 0.272
> 22 0.420
> 3 0.187
> 5 0.407
> 50 0.435
> 2 0.337
> 8 0.158
> 15 0.216
> 26 0.318
> 24 0.393
> 27 0.237
> 46 0.489
> 25 0.135
> 9 0.010 *
> 42 0.467
> 6 0.198
> 14 0.015 *
>
> Number of empty cells: 14Un certain nombre de patterns statistiquement significatifs est à prévoir. Les plus problématiques sont ceux ayant des fréquences observées fréquentes (les premières listées). Il est vraisemblable que les plus petites fréquences engendrent des contributions plus importantes. Une règle est de vérifier si le nombre de check est inférieur à 5% du nombre de pattern. Ici, il y 50 patterns, ce qui donne \(.05*50=2.5\) patterns et comme il n’y a que deux patterns statistiquement significatifs, \(2.5 > 2\), ces patterns peuvent être ignorés. Cependant, s’ils y a avait plus de checks touchant des patterns plus fréquent, il faudrait remédier à la situation, soit en retirant ou ajoutant des items ou, plus simplement, en augmentant le nombre de classes.
En effet, en plus de vérifier l’indépendance locale, l’inspection des patterns permet de vérifier l’adéquation du nombre de classes, car s’il y a trop peu de classes, il y aura beaucoup de patterns statistiquement significatifs.
22.1.4 Représentations graphiques
La représentation graphique des classes peut se faire facilement avec la fonction plot() en y mettant la sortie de poLCA().
plot(LCA3)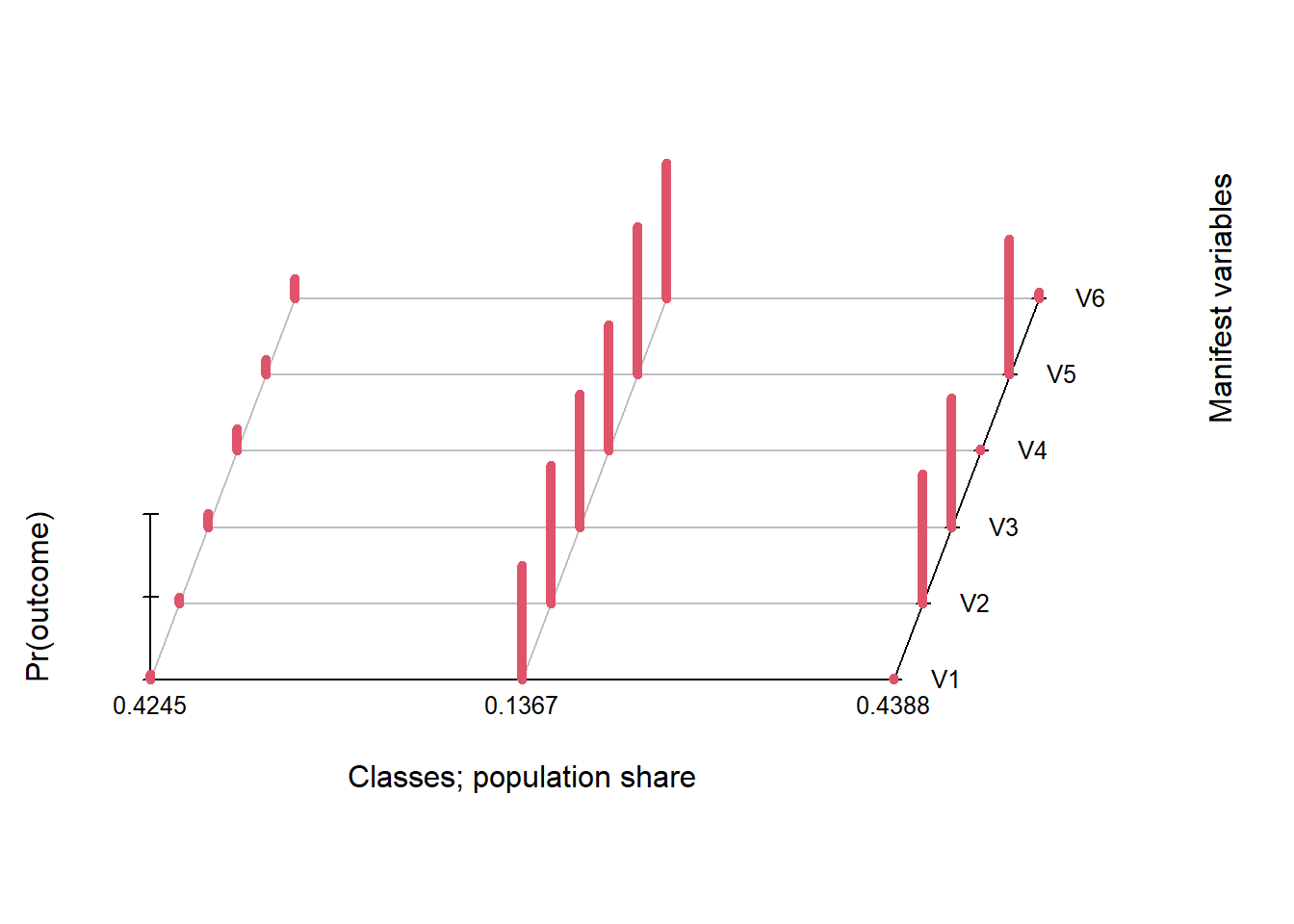
Figure 22.2: Analyse visuelle des classes
La Figure ?? montre sur l’axe des \(x\) (largeur), les classes avec les proportions, sur l’axe des \(z\) (profondeur), il s’agit des différents items utilisés pour la classification et sur l’axe des \(y\) la probabilité qu’une personne de la classe \(x\) ait choisi une certaine réponse à l’item \(z\). Si les items permettaient plus de choix de réponses (une échelle a plus deux options), la figure s’ajusterait en conséquences.
Une autre façon de présenter les données avec ggplot2 serait de programmer cette figure (à venir ultérieurement dans poLCAExtra).
#library(tidyverse)
#jdtest <- LCAE$LCA[[3]]$y
jdtest <- LCA3$y
v <- (colnames(jdtest))
jdtest$Classes <- as.factor(predict(LCA3)$Pred)
jdtest <- jdtest %>%
gather(key = "Variable", value = "Value", -Classes)
jds <- jdtest %>%
group_by(Classes, Variable) %>%
summarise(y = mean(Value),
se = sd(Value)/sqrt(n()),
ymin = y - 1.96*se,
ymax = y + 1.96*se,
Value = y)
> `summarise()` has grouped output by 'Classes'. You can
> override using the `.groups` argument.
jdtest %>%
ggplot(aes(x = Variable, y = Value, fill = Classes, group = Classes, color = Classes)) +
geom_jitter(alpha = .1) +
geom_point(jds, mapping = aes(x = Variable, y = y)) +
geom_errorbar(jds, mapping = aes(ymin = ymin, ymax = ymax), alpha = 1) + theme_minimal()
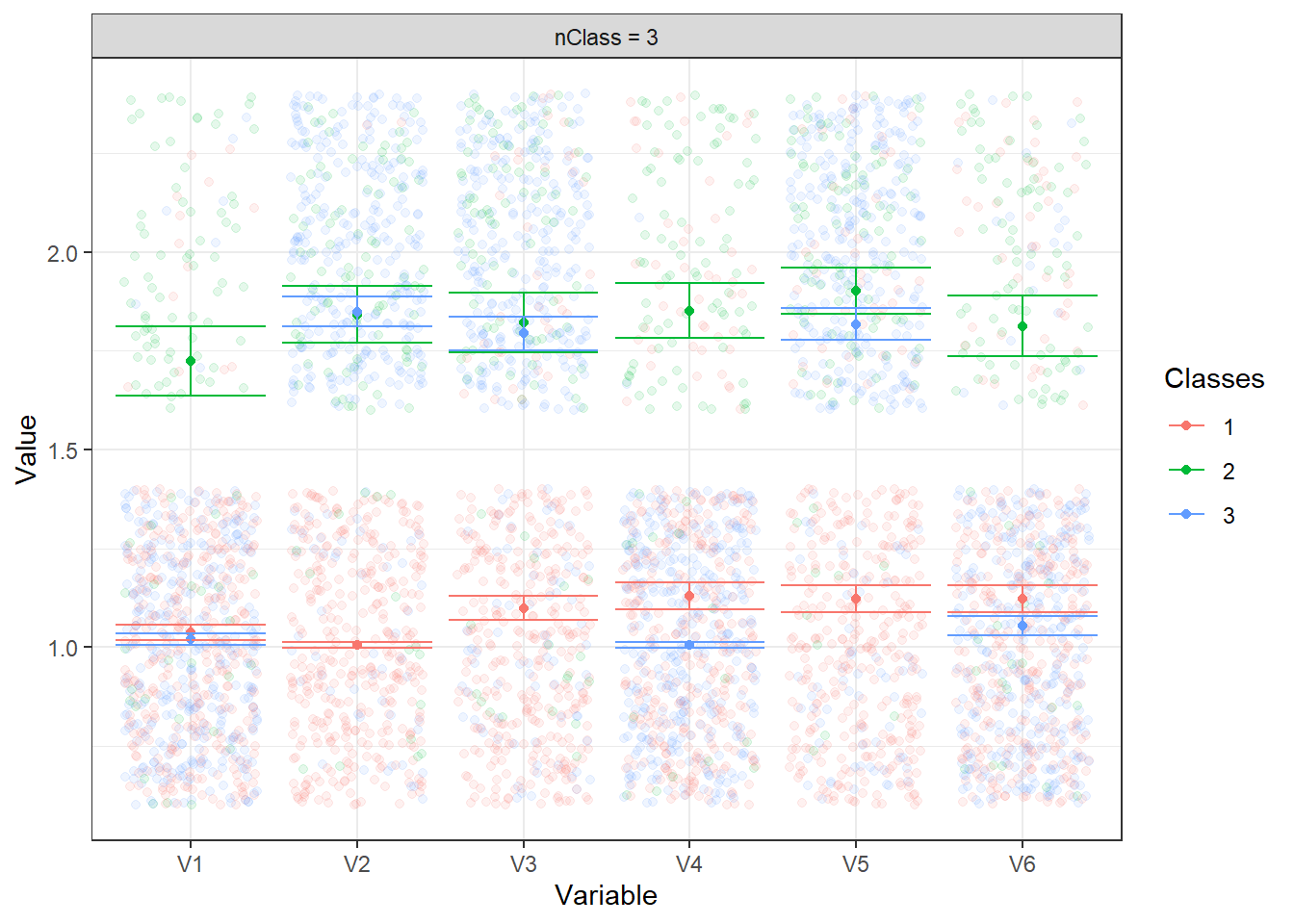
Figure 22.3: Analyse visuelle supplémentaire des classes
Cette méthode sera plus similaire à l’analyse de classes latentes.
22.1.5 Analyses supplémentaires
L’expérimentateur souhaite parfois tester si les classes se comparent sur d’autres variables. Dans ces cas, il faut tenir compte de la probabilité d’appartenir à l’une des classes et non pas utiliser uniquement la classe prédite (la plus probable). Cela entraînerait des biais statistiques. Par exemple, un participant ayant 33 %, 33 % et 34 %, se verrait attribuer à la troisième classe, même si, au fond, il pourrait bien appartenir à l’une des deux autres. Les analyses 3-step sont développées justement pour tenir compte de ces probabilité. Il y a deux fonctions principales r3step() pour les variables continues et d3step() pour les variables nominales et catégorielles.
Pour une variable à échelle continue, r3step() fonctionne avec la sortie avec le nombre approprié de classes ainsi que le nom de la variable dépendante ou une formule comme continue ~ 1.
res.r3 <- r3step("continuous", LCA3)Il est possible d’obtenir une représentation graphique ainsi.
plot(res.r3)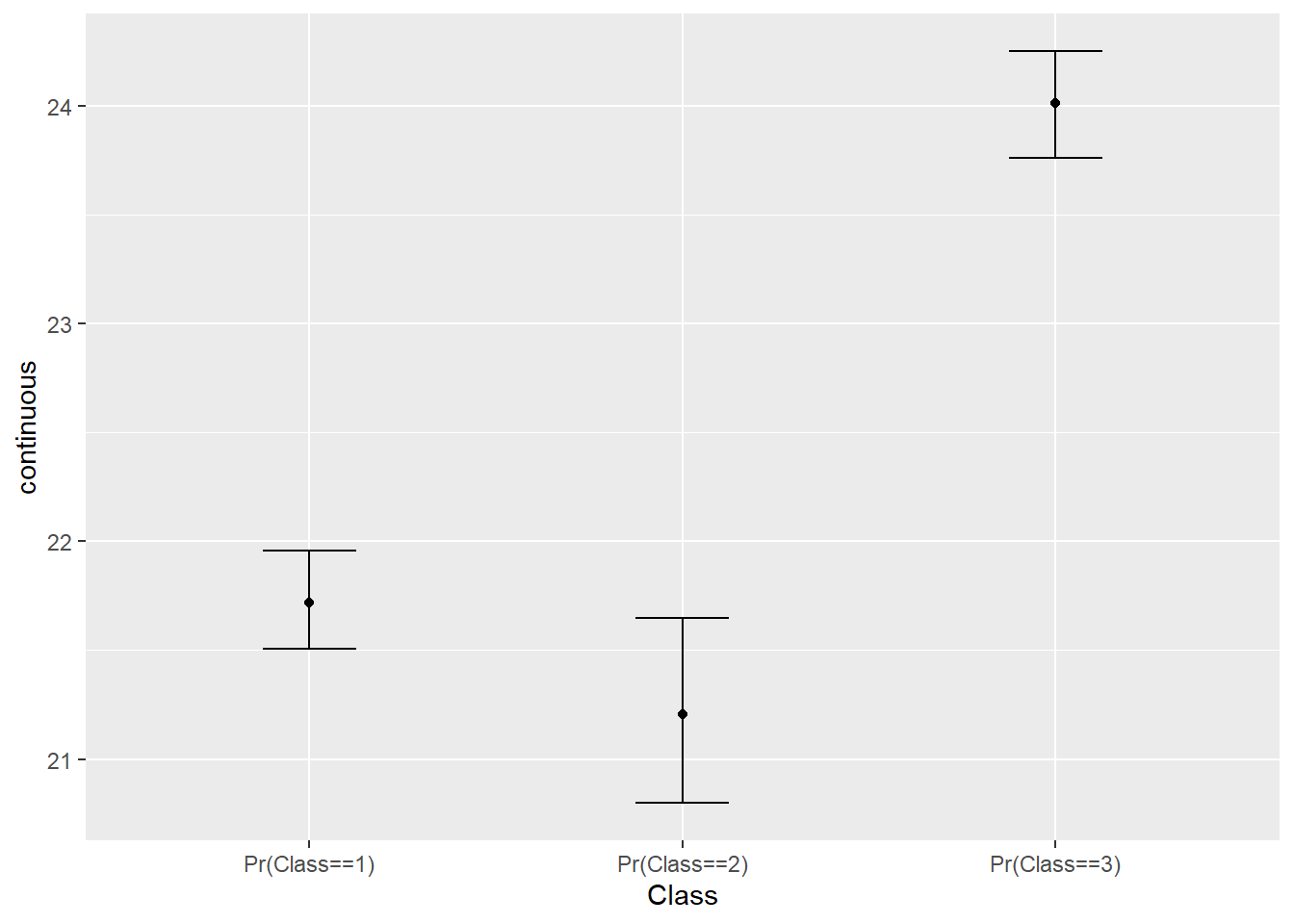
Figure 22.4: r3step des classes
Pour une variable à échelle nominale, d3step() fonctionne avec la sortie avec le nombre approprié de classes ainsi que le nom de la variable dépendante ou une formule comme categorical ~ 1.
res.d3 <- d3step("categorical", LCA3)Cette fonction possède aussi une représentation graphique.
plot(res.d3)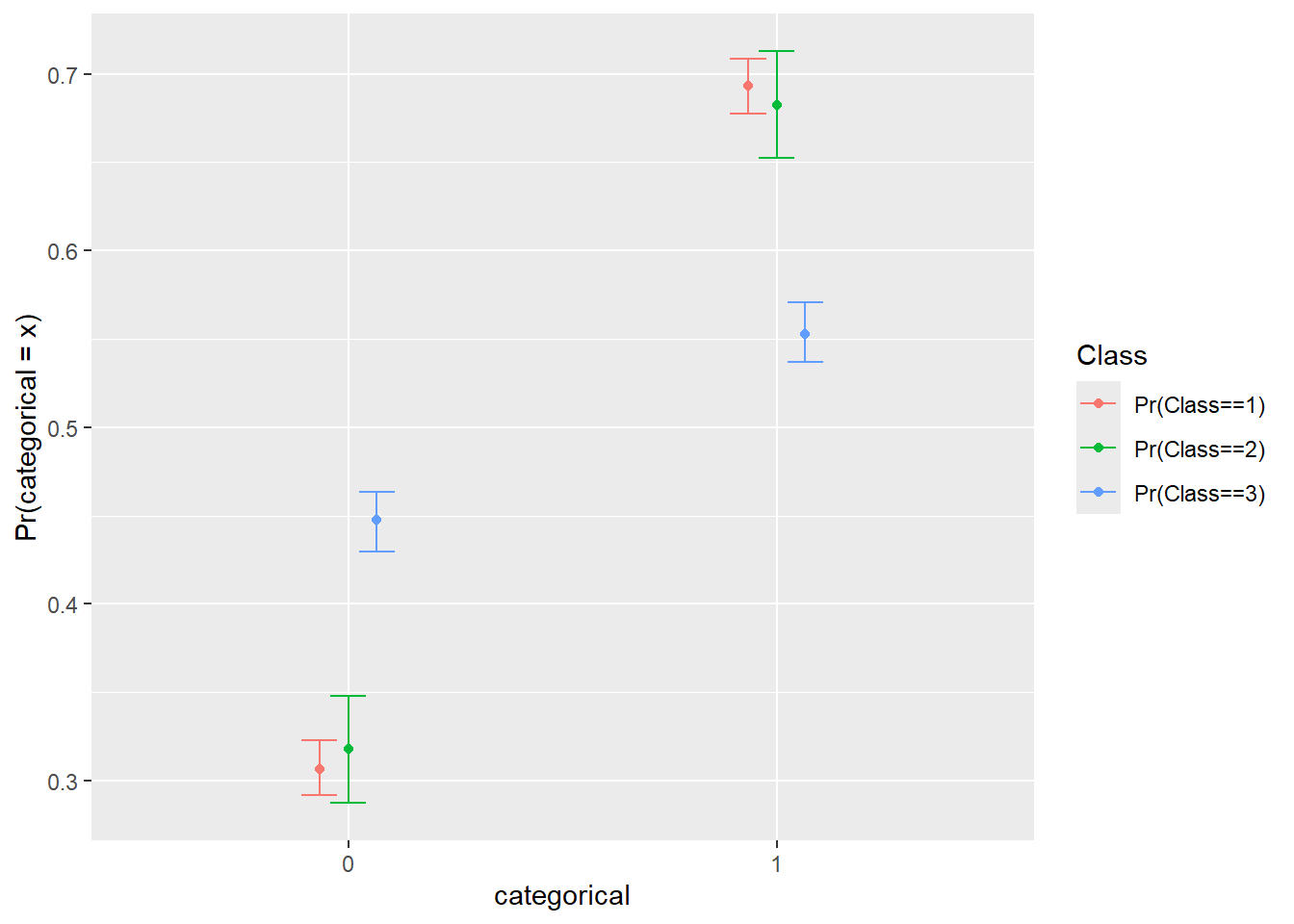
Figure 22.5: r3step des classes
22.1.6 Quelques conseils utiles
Une fois l’analyse terminée, il est recommander de rouler une dernière fois l’analyse avec une graine et les arguments nrep et maxiter pour s’assurer de la stabilité et de la répétabilité des résultats.
22.2 Profils latents
Pour les profils latents, le package suivant est nécessaire. Il faut d’abord l’installer, puis l’appeler.
Le package tidyLPA est compatible avec l’environnement du tidyverse.
Pour effectuer l’analyse de profils latents, il faut sélectionner les variables pour l’analyse avec la fonction select. Dans la fonction estimate_profiles, il faut spécifier le nombre de profils à investiguer. Ici, le jeu de données ex3.tidyLPA de poLCAExtra est utilisé.
jd <- ex3.tidyLPA
LPA1_5 <- jd %>%
select(V1, V2, V3, V4, V5) %>%
estimate_profiles(1:5)
LPA1_5
> tidyLPA analysis using mclust:
>
> Model Classes AIC BIC Entropy prob_min prob_max
> 1 1 7170.48 7207.52 1.00 1.00 1.00
> 1 2 5949.93 6009.19 0.96 0.98 0.99
> 1 3 4934.20 5015.68 1.00 1.00 1.00
> 1 4 4936.30 5040.00 0.91 0.62 1.00
> 1 5 4947.38 5073.31 0.82 0.39 1.00
> n_min n_max BLRT_p
> 1.00 1.00
> 0.35 0.65 0.01
> 0.33 0.33 0.01
> 0.08 0.33 0.20
> 0.06 0.33 0.99Comme les analyses de classes latentes, il faut procéder étape par étape pour déterminer le nombre de classes. Dans estimate_profiles(), on peut directement inscrire toutes les classes à investiguer. Le meilleur nombre de classes se base sur des AIC et BIC le plus bas possibles et une entropie relative42 de plus de .80. Il est aussi possible de se baser sur le BLRT_p, soit la valeur-\(p\) d’un test de ratio de vraisemblance bootstrapé (similaire au Lo-Mendell-Rubin présenté dans les classes latentes). Dans cet exemple
Il est possible de générer des graphiques pour comparer certains indices d’ajustement, notamment l’AIC, le BIC et l’entropie à l’aide de la fonction plot.
plot(LPA1_5, statistics = 'AIC')
plot(LPA1_5, statistics = 'BIC')
plot(LPA1_5, statistics = 'Entropy')Une fois le nombre de classes décidé, il faut rerouler l’analyse avec le nombre désiré.
LPA3 <- jd %>%
select(V1, V2, V3, V4, V5) %>%
estimate_profiles(3)Pour connaître le nombre de participants (n) dans chaque profil, il faut procéder ainsi.
get_data(LPA3) %>%
group_by(Class) %>%
count()
> # A tibble: 3 × 2
> # Groups: Class [3]
> Class n
> <dbl> <int>
> 1 1 100
> 2 2 100
> 3 3 100Finalement, il est possible générer la représentation graphique du modèle choisi (et des autres modèles si besoin) à l’aide de la fonction plot_profiles.
LPA3 %>%
plot_profiles()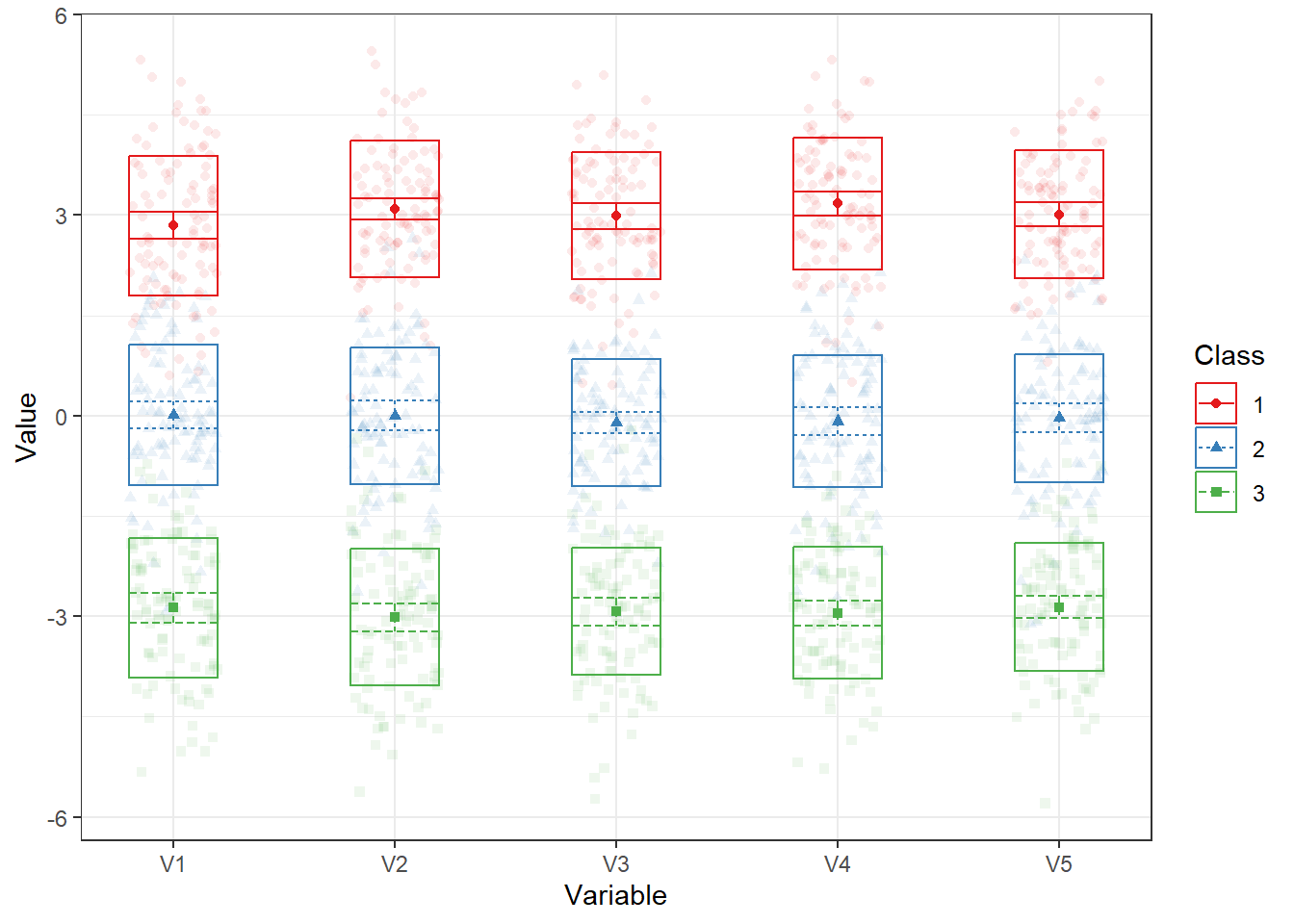
Figure 22.6: Analyse visuelle des profils
La Figure22.6 permet de visusalier le profil des réponses des participants selon les items.
Enfin, différents type de modèles sont possibles. Le package tidyLPA en dénombre six dont la Table 22.1 présente leurs caractéristiques.
| Model | Variance | Covariance |
|---|---|---|
| 1 | equal | zero |
| 2 | varying | zero |
| 3 | equal | equal |
| 4 | varying | equal |
| 5 | equal | varying |
| 6 | varying | varying |