19 Explorer

Comme il a été vu, l’analyse en composantes principales (ACP) fait partie de la famille des analyses factorielles exploratoires. Elle est exploratoire, car les loadings sont complètement libres. De plus, l’ACP n’impose pas de structure sur les données. Elle réorganise les variables corrélées (une matrice de covariance) en nouvelles variables orthogonales (décorrélées) les unes des autres (composantes). L’ACP n’informe pas du nombre de composantes signifiantes (importantes) dans le jeu de données. S’il y a \(p\) variables, elle réorganise la variance en \(p\) dimensions. Cependant, le statisticien opportuniste sait que l’information pertinente se trouve dans les valeurs propres les plus élevées et peut les utiliser pour résumer les données.

Le statisticien peut toutefois tenter d’isoler la structure factorielle sous-jacente aux données. Plutôt que de réorganiser la matrice de corrélation par une rotation géométrique, il peut tenter d’extraire des facteurs latents de cette matrice. Cette technique se nomme l’analyse factorielle exploratoire. Elle impose une structure aux données, soit un nombre de facteurs, mais demeure exploratoire, car les loadings restent libres.

À ce stade, il est intéressant de se pencher sur ce qu’est la structure factorielle sous-jacente à la matrice de corrélation avant d’expliquer l’analyse qui permet de la retrouver. La création de données aidera à en mieux comprendre les tenants et aboutissants.

19.1 Création de données

Pour construire un jeu de données ayant une structure factorielle, il faut d’abord concevoir cette structure. Il s’agit des loadings des facteurs³⁹. Il s’agit d’une matrice \(k \times p\), c’est-à-dire nombre de facteurs par nombre de variables.

Il est plus simple de considérer pour l’instant une structure standardisée, c’est-à-dire que les variables produites auront des variances de 1 (les moyennes sont écartées, car elles ne sont pas nécessaires). Lors de la spécification de la structure factorielle, il faut s’assurer que la somme des carrés des loadings de chaque variable ne dépasse pas \(1\), soit la variance désirée des variables. Ne pas respecter cette limite ne crée pas forcément une erreur. Seulement, le scénario ne sera plus standardisé.

La Figure 19.1 illustre un exemple de modèle. Les rectangles sont des variables manifestes (observées) à partir desquelles les variables encerclées représentent des facteurs sous-jacents, soit des variables latentes (retrouvées à partir des variables manifestes).

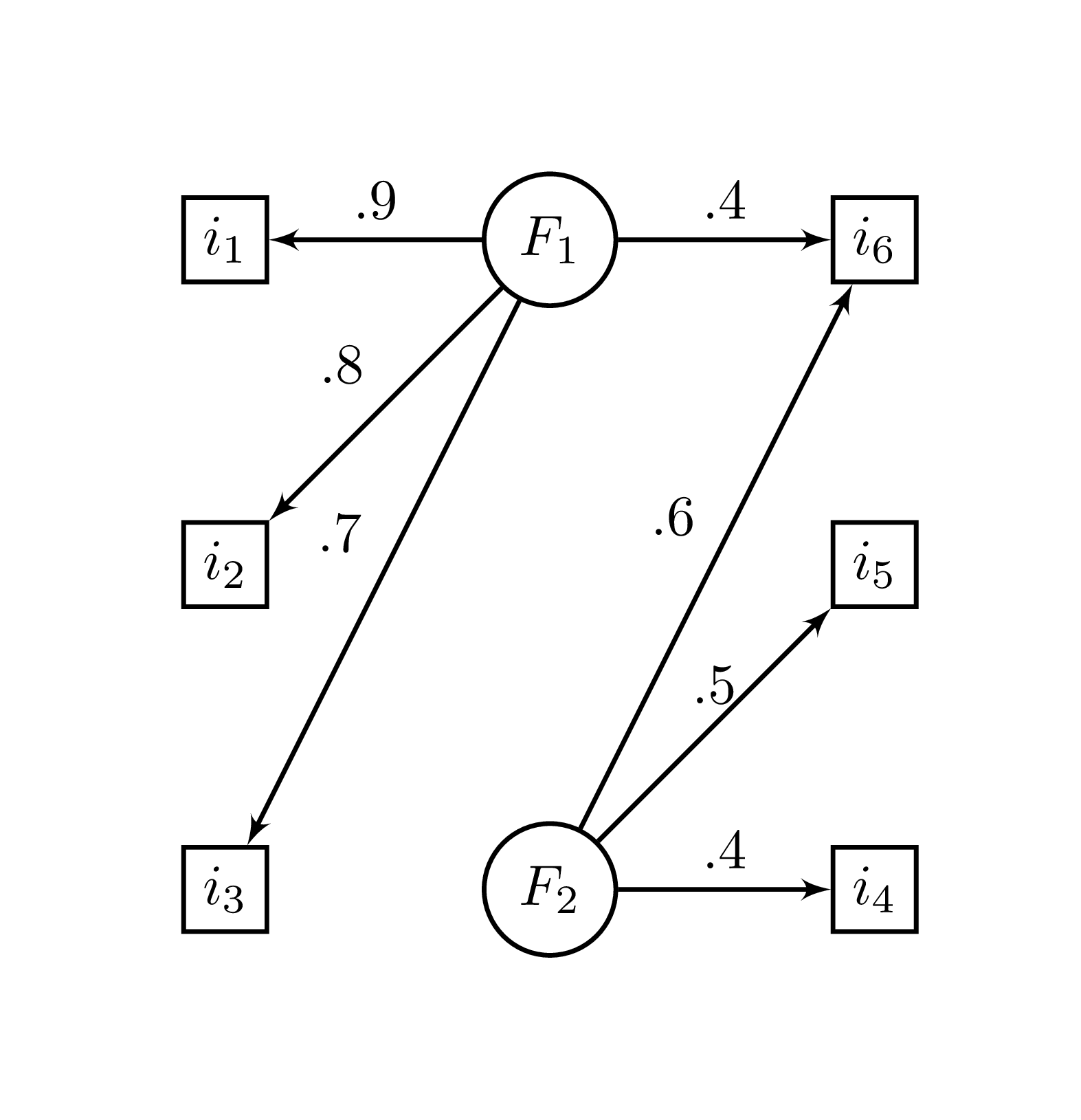
Figure 19.1: Structure factorielle

La syntaxe ci-dessous reconstruit le modèle de la Figure 19.1. La variable phi, pour \(\Phi\), contient les loadings des deux composantes pour créer les six variables. Les lignes (les variables) sont identifiées par i et les colonnes (les facteurs) sont identifiées par F.

# Création de la matrice de recette de fabrication
phi <- matrix(c(.9, .8, .7,  0,  0, .4,
                 0,  0,  0, .4, .5, .6), 
              nrow = 6, ncol = 2)

# Identification des variables et facteurs
colnames(phi) <- c("F1", "F2")
rownames(phi) <- paste0(rep("i",6), 1:6)
phi
>     F1  F2
> i1 0.9 0.0
> i2 0.8 0.0
> i3 0.7 0.0
> i4 0.0 0.4
> i5 0.0 0.5
> i6 0.4 0.6

19.1.1 Première technique

À partir de phi, il est possible d’obtenir la matrice de corrélation de la population \(\text{P}\) (\(\rho\) majuscule) par l’équation (19.1)

\[\begin{equation} \text{P} = \Phi \Phi^{\prime} \tag{19.1} \end{equation}\]

ou en code R.

R <- phi %*% t(phi)
R
>      i1   i2   i3   i4   i5   i6
> i1 0.81 0.72 0.63 0.00 0.00 0.36
> i2 0.72 0.64 0.56 0.00 0.00 0.32
> i3 0.63 0.56 0.49 0.00 0.00 0.28
> i4 0.00 0.00 0.00 0.16 0.20 0.24
> i5 0.00 0.00 0.00 0.20 0.25 0.30
> i6 0.36 0.32 0.28 0.24 0.30 0.52

Le lecteur attentif aura remarqué qu’il ne s’agit pas encore d’une matrice de corrélation : la diagonale n’est pas constituée de 1. Le résultat de \(\Phi\Phi^{\prime}\) représente la matrice de corrélation réduite.

Il reste à ajouter le bruit, la variance résiduelle, ce qui est fait en changeant la diagonale de \(R\) pour l’unité, \(\text{diag}(R) = 1\). D’ailleurs, si une valeur de la diagonale R dépasse 1, alors le scénario standardisé n’est pas respecté. Il s’agit d’une des méthodes pour s’en assurer.

diag(R) <- 1
R
>      i1   i2   i3   i4  i5   i6
> i1 1.00 0.72 0.63 0.00 0.0 0.36
> i2 0.72 1.00 0.56 0.00 0.0 0.32
> i3 0.63 0.56 1.00 0.00 0.0 0.28
> i4 0.00 0.00 0.00 1.00 0.2 0.24
> i5 0.00 0.00 0.00 0.20 1.0 0.30
> i6 0.36 0.32 0.28 0.24 0.3 1.00

Avec la matrice R calculée, il est évidemment possible, comme il a été fait précédemment de recourir à la fonction MASS::mvrnorm() avec comme argument Sigma = R pour la matrice de corrélation afin de créer n participants. Il ne reste qu’à choisir une taille d’échantillon.

# Pour la reproductibilité
set.seed(33)

# Création du jeu de données
jd <- MASS::mvrnorm(n = 50, 
                    mu = rep(0, ncol(R)), 
                    Sigma = R)
head(jd)
>           i1     i2      i3     i4      i5     i6
> [1,]  0.0147 -0.464  0.5397  1.187 -0.2932  0.335
> [2,] -0.4613 -0.288  0.0302  0.960  1.2070  0.789
> [3,] -1.1191 -0.980 -0.2839 -0.684  0.0166 -0.700
> [4,] -0.2842  0.619  0.0473 -1.013  0.8804  0.139
> [5,]  1.0263  2.322  1.4843  2.451 -0.5138  1.936
> [6,] -0.6026 -0.569 -0.5789 -1.501  2.2906  0.157

19.1.2 Deuxième technique

Passer par MASS::mvrnorm() est toutefois contre-productif, puisque la fonction mvrnorm() utilise l’ACP pour extraire une structure factorielle pour ensuite générer les données. Une autre façon de créer des données est en passant par la loi de la somme des variances. Chaque loading \(\phi_k\) d’une variable \(x_i\) est dans ce contexte [une constante d’échelle][Ajout des constantes d’échelle \(\beta\)] jointe à un score factoriel normalement distribué \(z_k\). L’équation (19.2) représente cette relation.

\[\begin{equation} x_i = \phi_1 z_1 + ... + \phi_k z_k + \epsilon \tag{19.2} \end{equation}\]

Ce qui rappelle le modèle linéaire général de l’équation (14.19) (section Prédire). La variable \(\epsilon\) correspond à la variance résiduelle, c’est-à-dire la part de variance de la variable non expliquée par les facteurs.

En désirant le scénario standardisé, la variance de \(x\) est fixée à 1 et isoler \(\epsilon\) pour en déterminer la variance garantit ce scénario. Cela revient à calculer l’équation (19.3).

\[\begin{equation} \sigma^2_\epsilon = 1 - (\phi_1^2 + ... + \phi_k^2) \tag{19.3} \end{equation}\]

Les écarts types des \(\epsilon\) de chaque \(p\) variable de la structure factorielle phi se calculent simplement avec R.

sd.eps <- sqrt(1 - rowSums(phi^2))

Maintenant, il faut ajouter cette variable à la structure factorielle. Comme les résidus sont tous indépendants par définition, ils ont tous leur propre facteur (chacun sa colonne), ce qui se fait bien avec la syntaxe suivante.

diag(sd.eps)
>       [,1] [,2]  [,3]  [,4]  [,5]  [,6]
> [1,] 0.436  0.0 0.000 0.000 0.000 0.000
> [2,] 0.000  0.6 0.000 0.000 0.000 0.000
> [3,] 0.000  0.0 0.714 0.000 0.000 0.000
> [4,] 0.000  0.0 0.000 0.917 0.000 0.000
> [5,] 0.000  0.0 0.000 0.000 0.866 0.000
> [6,] 0.000  0.0 0.000 0.000 0.000 0.693

Il suffit maintenant de joindre cette matrice à phi.

phi2 <- cbind(phi, diag(sd.eps))

Il est tentant de joindre directement le vecteur sd.eps à phi. Par contre, joindre ce vecteur comme cbind(phi, sd.eps) implique une structure à trois facteurs : les résidus sont corrélés par les loadings de ce troisième facteur. En utilisant diag(se.eps), chaque résidu à son propre facteur et est indépendant des autres. La structure finale possède \(k\) (nombre de facteurs, 2 dans cet exemple) communs en plus de \(p\) (nombre de variables, 6 dans cet exemple) facteurs résiduels et ainsi \(k + p\) dimensions.

Comme à l’équation (19.1), phi2 permet d’obtenir la matrice de corrélation de la population.

R2 <- phi2 %*% t(phi2)
R2
>      i1   i2   i3   i4  i5   i6
> i1 1.00 0.72 0.63 0.00 0.0 0.36
> i2 0.72 1.00 0.56 0.00 0.0 0.32
> i3 0.63 0.56 1.00 0.00 0.0 0.28
> i4 0.00 0.00 0.00 1.00 0.2 0.24
> i5 0.00 0.00 0.00 0.20 1.0 0.30
> i6 0.36 0.32 0.28 0.24 0.3 1.00

Exactement le même résultat que l’autre méthode, et ce, sans avoir à modifier la diagonale par l’unité. Les variances résiduelles sont déjà calculées.

Une fois la structure factorielle obtenue, il faut générer les scores des participants (les valeurs \(z\) de l’équation (19.2)). Une technique usuelle est de créer une matrice \((k + p) \times n\) de scores normaux, soit le nombre de facteurs plus le nombre de variables (pour les résidus) en ligne par \(n\) le nombre d’unités en colonnes. Cette matrice représente les scores factoriaux de chaque unité pour chacun des scores et sont multipliés avec la structure factorielle. Autrement dit, chaque poids (loadings) est multiplié à une distribution normale qui représente le score du participant pour ce facteur.

n <- 500; k <- 2; p <- 6
score.ind <-  matrix(rnorm(n * p * k), 
                     nrow = (k + p), 
                     ncol = n)
> Warning in matrix(rnorm(n * p * k), nrow = (k + p), ncol =
> n): data length differs from size of matrix: [6000 != 8 x
> 500]

Il ne reste plus qu’à faire le produit matricielle de phi2 (\(\left[ \Phi, \text{diag}(\epsilon) \right]\)) et des scores individuels (score.ind).

jd2 <- phi2 %*% score.ind

La variable jd2 contient tous les scores des \(n\) participants sur les \(p\) variables. Pour obtenir la base de données dans le sens usuel, il suffit de faire une transpose à jd avec la fonction t().

jd2 <- t(jd2)
head(jd2)
>          i1     i2      i3      i4     i5     i6
> [1,]  0.111 -0.886 -0.9769  0.5398  1.562  1.698
> [2,] -1.332 -0.808 -1.0043  0.0559  0.372 -1.006
> [3,] -1.451 -1.331 -1.7075  0.4404 -1.145 -2.224
> [4,]  0.439 -0.528  1.4282 -0.8922  0.437 -0.076
> [5,] -0.387 -0.488 -0.0509  0.5412  0.346 -0.262
> [6,]  0.526  1.163  0.2766  0.1620  0.747  0.944

Voilà une base de données prêtes à être utiliser pour une analyse factorielle. En pratique, pour donner un peu plus de réalisme, il est possible d’ajouter une moyenne (additionner), de modifier l’écart type (multiplier) de chacune des variables, d’arrondir les scores, et plus en fonction des besoins.

19.1.3 L’analyse en composantes principales

À titre de comparaison, voici les résultats de l’analyse en composantes principales.

# Analyse en composantes principales
res <- eigen(cor(jd2))
res
> eigen() decomposition
> $values
> [1] 2.503 1.340 0.888 0.588 0.427 0.253
> 
> $vectors
>         [,1]   [,2]    [,3]    [,4]    [,5]     [,6]
> [1,] -0.5659  0.133  0.0015  0.0729 -0.1699  0.79231
> [2,] -0.5394  0.129  0.1006  0.0207 -0.6224 -0.54259
> [3,] -0.5118  0.143 -0.0587  0.3666  0.7118 -0.27061
> [4,] -0.0330 -0.555  0.7725  0.3039  0.0111  0.04282
> [5,] -0.0431 -0.629 -0.6206  0.4303 -0.1780 -0.00138
> [6,] -0.3520 -0.491 -0.0676 -0.7631  0.2128 -0.05277

# Les deux premières valeurs propres

# Les loadings des deux premières composantes
ld <- res$vectors[,1:2] %*% 
  diag(sqrt(res$values)[1:2])
ld
>         [,1]   [,2]
> [1,] -0.8954  0.154
> [2,] -0.8534  0.149
> [3,] -0.8097  0.165
> [4,] -0.0522 -0.642
> [5,] -0.0682 -0.729
> [6,] -0.5569 -0.568

Elle est assez près de la structure originale, mais pas exactement. Et ce n’est pas à cause du relativement petit n ou de la graine. La cause est bel et bien que l’objectif de l’ACP est de réorganiser la variance plutôt que de rechercher une structure factorielle. L’ACP ne sait pas que la vraie structure contient des facteurs communs entre les variables. Pour tester la présence de facteurs communs, il faut procéder avec une autre analyse : l’analyse factorielle exploratoire (AFE).

19.2 Analyse factorielle exploratoire

Pour réaliser une analyse factorielle exploratoire, la fonction factanal() de R prend un jeu de données et le nombre de facteurs à tester. La fonction détecte automatiquement s’il s’agit d’un jeu de données ou une matrice de covariance; l’un ou l’autre peut être fourni.

res1 <- factanal(jd2, factors = 1)
res1
> 
> Call:
> factanal(x = jd2, factors = 1)
> 
> Uniquenesses:
>    i1    i2    i3    i4    i5    i6 
> 0.156 0.376 0.487 1.000 1.000 0.851 
> 
> Loadings:
>    Factor1
> i1  0.919 
> i2  0.790 
> i3  0.716 
> i4        
> i5        
> i6  0.386 
> 
>                Factor1
> SS loadings      2.131
> Proportion Var   0.355
> 
> Test of the hypothesis that 1 factor is sufficient.
> The chi square statistic is 86.9 on 9 degrees of freedom.
> The p-value is 6.84e-15

C’est aussi simple que l’ACP (même plus!). La sortie procure trois statistiques d’intérêt : les loadings, la proportion de variance expliquée (Proportion Var) et un test de \(\chi^2\) avec sa valeur-\(p\). Les loadings entre -.1 et .1 ne sont pas affichés afin d’attirer l’attention sur la structure. Les loadings peuvent être extraits avec la fonction loadings() ou en élément de liste. L’utilisation de [] permet d’afficher complètement la matrice de loadings.

loadings(res1)
> 
> Loadings:
>    Factor1
> i1  0.919 
> i2  0.790 
> i3  0.716 
> i4        
> i5        
> i6  0.386 
> 
>                Factor1
> SS loadings      2.131
> Proportion Var   0.355
res1$loadings[]
>    Factor1
> i1  0.9187
> i2  0.7896
> i3  0.7165
> i4 -0.0140
> i5 -0.0124
> i6  0.3864

La valeur-\(p\) concerne la qualité de de l’ajustement de la strucuture à factors facteurs. Comme la valeur-\(p\) est significative à un facteur, \(p < .001\), cela signifie que la structure testée (un facteur) n’est pas vraisemblable. Il faut tester pour deux facteurs.

res2 <- factanal(jd2, factors = 2)
res2
> 
> Call:
> factanal(x = jd2, factors = 2)
> 
> Uniquenesses:
>    i1    i2    i3    i4    i5    i6 
> 0.154 0.378 0.487 0.910 0.849 0.288 
> 
> Loadings:
>    Factor1 Factor2
> i1  0.920         
> i2  0.788         
> i3  0.716         
> i4          0.298 
> i5          0.387 
> i6  0.373   0.757 
> 
>                Factor1 Factor2
> SS loadings      2.121   0.812
> Proportion Var   0.354   0.135
> Cumulative Var   0.354   0.489
> 
> Test of the hypothesis that 2 factors are sufficient.
> The chi square statistic is 5.31 on 4 degrees of freedom.
> The p-value is 0.257

Les mêmes statistiques, mais pour deux facteurs, sont obtenues. Les résultats sont très près de la structure originale. La valeur-\(p\) n’est plus significative, ce qui suggère que le modèle semble bien de deux facteurs.

19.2.1 Extraire les scores

Une fois le nombre de facteurs déterminé (voir Réduire à ce sujet), les scores factoriels des participants peuvent être utilisés. Pour les obtenir, il faut commander de nouveau l’analyse factorielle en y indiquant le type de scores désiré, soit regression ou Bartlett. Cela ajoutera les scores dans la liste de sortie de la fonction sous l’appellation scores. Voici un exemple.

# Commander l'analyse avec l'argument scores = "regression"
res2 <- factanal(jd2, factors = 2, scores = "regression")

# Les scores factoriels se retouvent dans la sortie
head(res2$scores)
>      Factor1 Factor2
> [1,]  -0.244  1.7256
> [2,]  -1.259 -0.4500
> [3,]  -1.588 -1.5611
> [4,]   0.384 -0.2586
> [5,]  -0.399 -0.0404
> [6,]   0.667  0.7026

19.3 Calculs de l’analyse factorielle exploratoire

Il existe deux techniques plus connues pour réaliser l’analyse factorielle exploratoire : la factorisation en axes principaux (PAF; principal axis factoring) et l’analyse factorielle par maximum de vraisemblance (MLFA; maximum likelihood factor analysis).

La PAF tente de retrouver la matrice de corrélation originale sans bruit, c’est-à-dire la matrice de corrélation réduite dans laquelle la diagonale n’est pas constituée de \(1\) soit phi %*% t(phi) (en code) ou \(\Phi\Phi^\prime\) (en équation). Elle se base sur l’ACP (la fonction maison ci-dessous utilise eigen()) avec quelques raffinements supplémentaires.

La logique est de prendre les loadings \(\phi\) d’un nombre arbitraire de \(k\) facteurs, puis de calculer la communalité des variables, soit l’équation (19.4) pour la variable \(i\)

\[\begin{equation} C_i = \sum_{i=1}^k \Phi_i^2 \tag{19.4} \end{equation}\]

pour enfin soustraire de deux communalités subséquentes la différence jusqu’à ce que celle-ci converge le plus près possible de 0 (donc, virtuellement aucune différence entre les deux communalités). Autrement dit, l’objectif de la PAF est de retrouver la matrice de corrélation réduite.

Pour ce faire, il faut utiliser une technique itérative. En optimisation, il faut prendre quelques précautions pour s’assurer du bon fonctionnement du logiciel :

• fixer un maximum d’itérations afin de s’assurer d’éviter d’entrer dans une boucle interminable duquel le logiciel ne peut s’échapper;

• fixer un seuil de convergence à atteindre afin de déterminer une fin à l’optimisation.

Ces deux règles évitent aux programmeurs de fixer son écran pendant des heures pendant lesquelles le programme calcule des résultats de boucles interminables.

Ces deux recommandations se retrouvent en arguments et peuvent être modifiées

paf <- function(covmat, 
                nfactors, 
                converge = .000001, 
                max.iter = 100){
  
  # Nombre de variables
  p <- ncol(covmat)
  
  # Boucle d'estimation avec itérations
  # maximales (max.iter)
  for(i in 1:max.iter){
    
    # ACP de la matrice
    res <- eigen(covmat)
    
    # Les loadings
    ld <- res$vector[,1:nfactors] %*% 
      sqrt(diag(res$values[1:nfactors], ncol = nfactors))
    
    # Les communalités
    co <- rowSums(ld^2)
    
    # La différence à optimiser
    diff <- diag(covmat) - co
    
    # Si toutes les différences sont plus petites que
    # `convergence`, alors `break` cesse la boucle
    if (all(abs(diff) < converge)) break
    
    # Si non,
    # mettre à jour la nouvelle diagonale
    # de la matrice et continuer
    covmat <- covmat - diag(diff)
  }
  
  # Sortie
  return(list(uniquenesses = 1-co,
              loadings = ld,
              covmat = covmat))
}

Noter l’ajout de ncol = dans la fonction diag(). Cela a pour but de forcer R à créer une matrice \(1 \times 1\)⁴⁰. Enfin, noter l’introduction de break (aperçu dans la section Les variables) qui permet de mettre fin à une boucle lorsque une condition est atteinte.

À toute fin de comparaison, voici la technique PAF maison (paf()) et l’analyse factorielle de R.

factanal(covmat = R, n.obs = n, factors = 2)
> 
> Call:
> factanal(factors = 2, covmat = R, n.obs = n)
> 
> Uniquenesses:
>   i1   i2   i3   i4   i5   i6 
> 0.19 0.36 0.51 0.84 0.75 0.48 
> 
> Loadings:
>    Factor1 Factor2
> i1  0.899         
> i2  0.799         
> i3  0.699         
> i4          0.399 
> i5          0.499 
> i6  0.368   0.620 
> 
>                Factor1 Factor2
> SS loadings      2.071   0.799
> Proportion Var   0.345   0.133
> Cumulative Var   0.345   0.478
> 
> Test of the hypothesis that 2 factors are sufficient.
> The chi square statistic is 0 on 4 degrees of freedom.
> The p-value is 1
paf(covmat = R, nfactors = 2)
> $uniquenesses
> [1] 0.19 0.36 0.51 0.84 0.75 0.48
> 
> $loadings
>         [,1]   [,2]
> [1,] -0.8865 -0.155
> [2,] -0.7880 -0.138
> [3,] -0.6895 -0.121
> [4,] -0.0689  0.394
> [5,] -0.0862  0.493
> [6,] -0.4974  0.522
> 
> $covmat
>      i1   i2   i3   i4   i5   i6
> i1 0.81 0.72 0.63 0.00 0.00 0.36
> i2 0.72 0.64 0.56 0.00 0.00 0.32
> i3 0.63 0.56 0.49 0.00 0.00 0.28
> i4 0.00 0.00 0.00 0.16 0.20 0.24
> i5 0.00 0.00 0.00 0.20 0.25 0.30
> i6 0.36 0.32 0.28 0.24 0.30 0.52

Les résultats sont très près, beaucoup plus que l’ACP de la matrice R. La sortie uniqueness correspond à 1-C, la variance résiduelle. Dans les cas, elles sont virtuellement identiques. Dans la sortie de paf(), la matrice de corrélation réduite de R est sortie et montre qu’elle correspond à ce qui est attendu, soit \(\Phi\Phi^{\prime}\).

phi %*% t(phi)
>      i1   i2   i3   i4   i5   i6
> i1 0.81 0.72 0.63 0.00 0.00 0.36
> i2 0.72 0.64 0.56 0.00 0.00 0.32
> i3 0.63 0.56 0.49 0.00 0.00 0.28
> i4 0.00 0.00 0.00 0.16 0.20 0.24
> i5 0.00 0.00 0.00 0.20 0.25 0.30
> i6 0.36 0.32 0.28 0.24 0.30 0.52
paf(covmat = R, nfactors = 2)$covmat
>      i1   i2   i3   i4   i5   i6
> i1 0.81 0.72 0.63 0.00 0.00 0.36
> i2 0.72 0.64 0.56 0.00 0.00 0.32
> i3 0.63 0.56 0.49 0.00 0.00 0.28
> i4 0.00 0.00 0.00 0.16 0.20 0.24
> i5 0.00 0.00 0.00 0.20 0.25 0.30
> i6 0.36 0.32 0.28 0.24 0.30 0.52

Les résultats sont toutefois légèrement différents pour les loadings. Cela est dû au fait que factanal() n’utilise pas la méthode PAF, mais bien le MLFA. Cette technique n’est pas détaillée ici. Elle est très similaire à PAF à l’exception qu’elle focalise sur l’estimation des loadings pour dériver les communalités, plutôt que d’utiliser seulement les communalités. Pour produire une fonction similaire, il faut passer par l’optimisation avec optim() (vue dans Les calculs de l’analyse en composantes principales).

19.4 Rapporter l’analyse factorielle

Lorsqu’il faut rapporter l’analyse factorielle, plusieurs éléments peuvent être rapportés dont certains varient fonction des habitudes du domaine de recherche. Les informations cruciales qu’il faut fournir sont les variances expliquées par chacun des facteurs retenus (Proportion Var ou Cumulative Var dans factanal() ou les communalités avec l’ACP). Le deuxième éléments sont les loadings de la structure finale avec ou sans les loadings négligeables, c’est-à-dire ceux de faible amplitude, comme le fait factanal() qui exclut les loadings de moins de .1 par défaut. Le tableau de loadings rapporté peut exclure les plus petits que .1, .3 ou .4, selon les recommandations psychométriques du domaine. Il est possible également de tous les conserver. Enfin, si une procédure de détermination du nombre de facteurs est utilisé (voir la prochaine section Réduire), la ou les méthodes sélectionnées ainsi que leur résultats sont rapportés. Autrement, il faut justifier le nombre de facteurs retenus.